Ansys Zemax | 如何模拟自适应光学系统

这篇文章介绍了如何在OpticStudio中使用多重结构创建反射式自适应光学系统。本文详细介绍了： 如何通过缩放光阑镜面的偏心来模拟一组镜面阵列 如何使用公差功能生成随机的波前差来模拟大气不均匀性对成像的影响 如何补偿该影响引入的像差以得到最优的几何和衍射点扩散函数 如何使用求解功能简化系统的设置和调整参数的过程

下载

联系工作人员获取附件

介绍

在本文介绍的自适应反射光学系统中，反射抛物镜由多个子反射镜组成，其中每个子反射镜可以调整自身的空间位置和旋转方向来一定程度的矫正像差。特别是对于处在大气环境中的望远镜系统来说，自适应系统可以有效的降低大气层不均匀性引入的像差。OpticStudio可以在非序列或混合序列模式下模拟自适应反射光学系统。本文将展示如何在序列模式下使用多重结构对该系统进行建模。 下图两幅动画展示了序列模式下自适应光学系统中反射元件的倾斜和偏心：

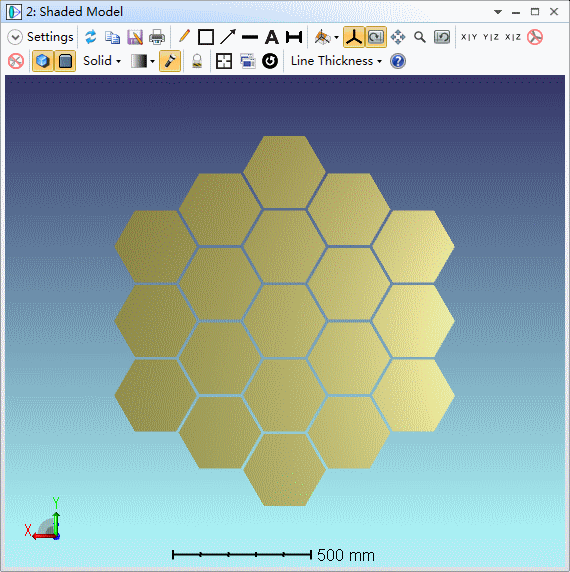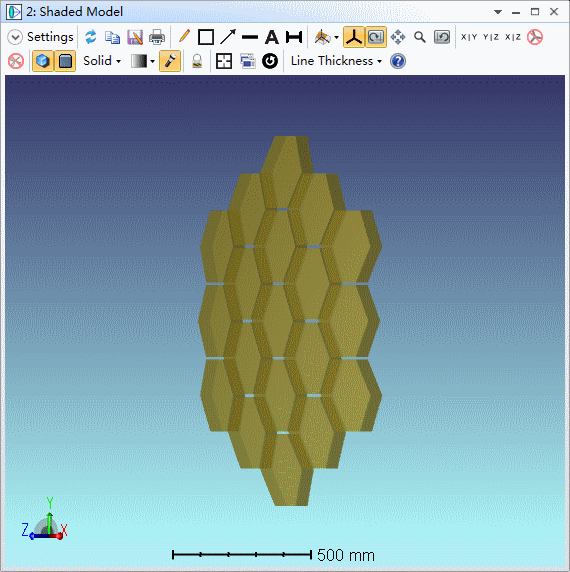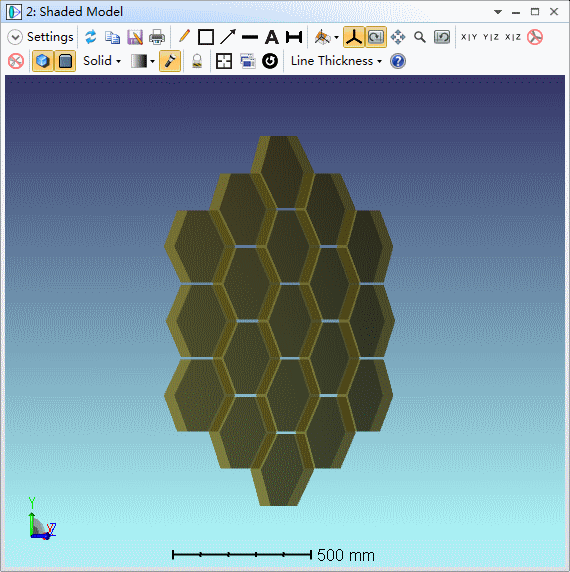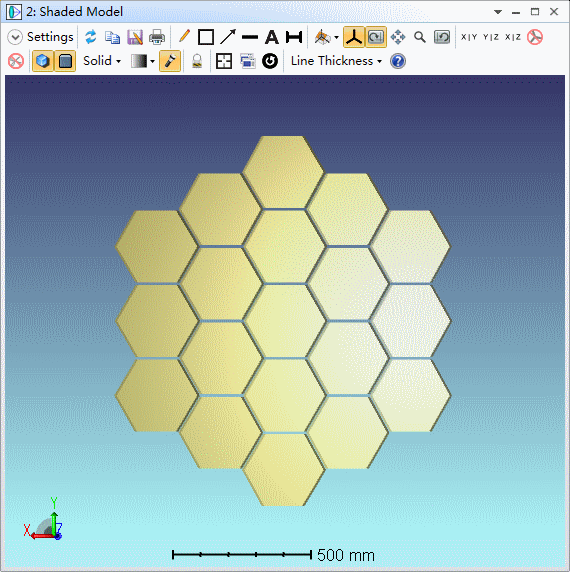
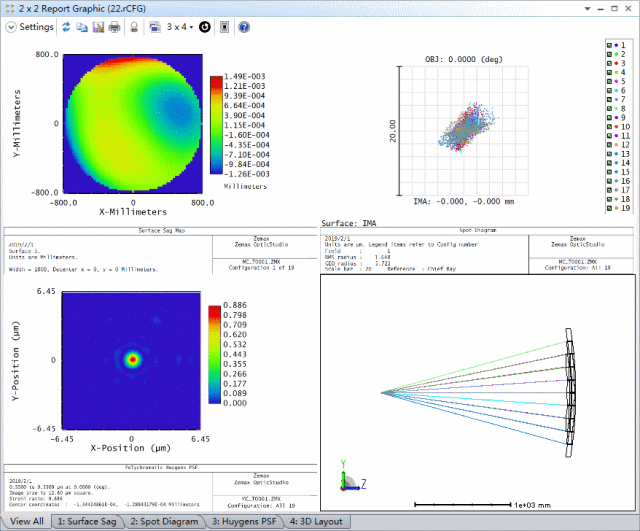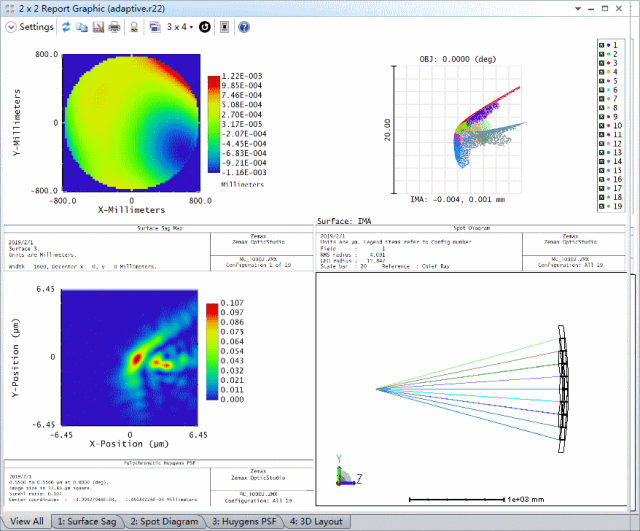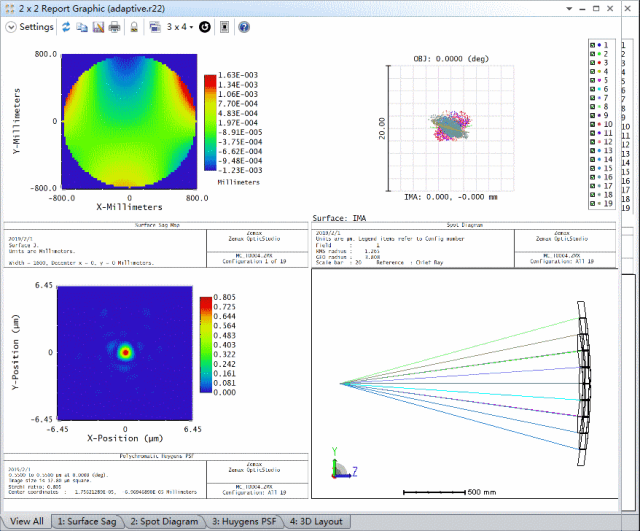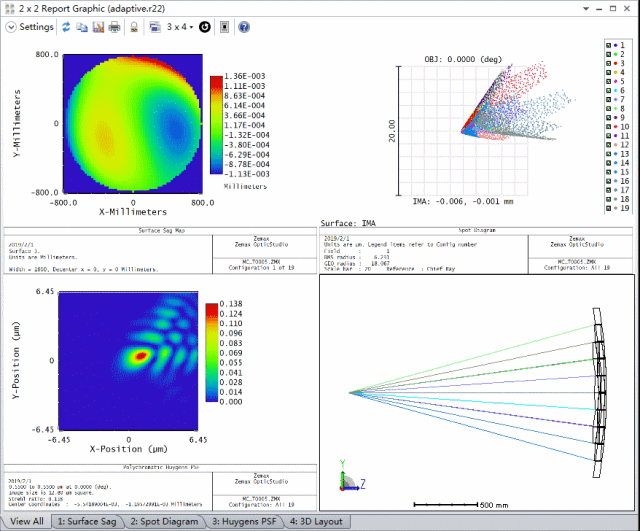
首先，我们需要在系统输入波前上引入随机的波前差来模拟大气不均匀性对输入光的影响。其次，我们需要调整每个反射元件的z轴位置以及绕元件中点的旋转角度，使像面上的像差最小。在下图给出的2x2报告图 (2x2 Report Graphic) 中，左上图描述了系统在输入波前上引入的随机像差，它是由蒙特卡洛算法自动生成的随机波前差。其中，其它图表动画对比了不同输入波前差的情况下，自适应光学系统矫正像差之前和之后的几何PSF和衍射PSF分析结果。

前提假设和设计目标

对于本文示例系统，我们作如下前提假设： 我们将只模拟望远镜的主镜，即反射抛物面。不考虑望远镜系统中的其他元件，例如次级反射镜等。这主要是为了减少示例的复杂度，但如果需要分析也可以快速添加。
每个子镜面不会产生形变。这同样是为了减少示例的复杂度，如需要也可快速添加。
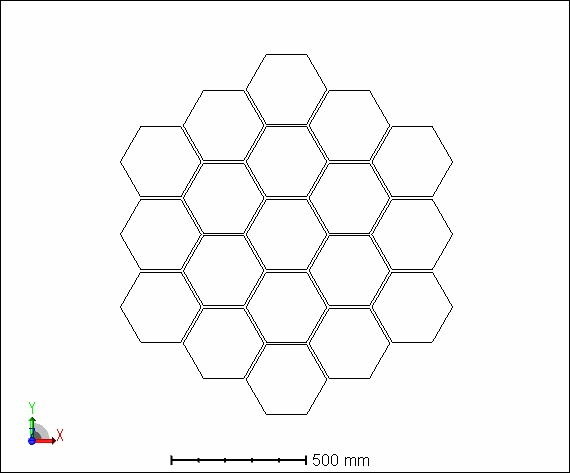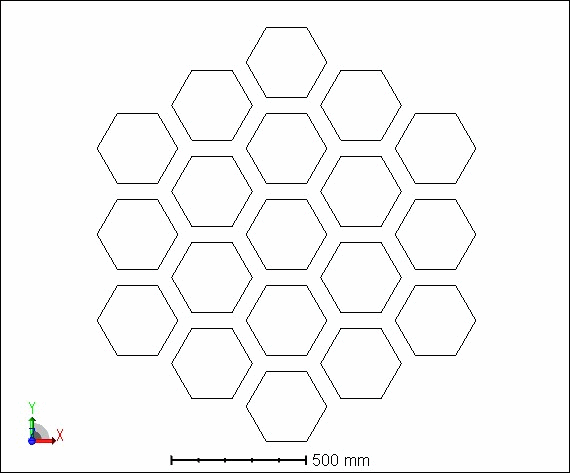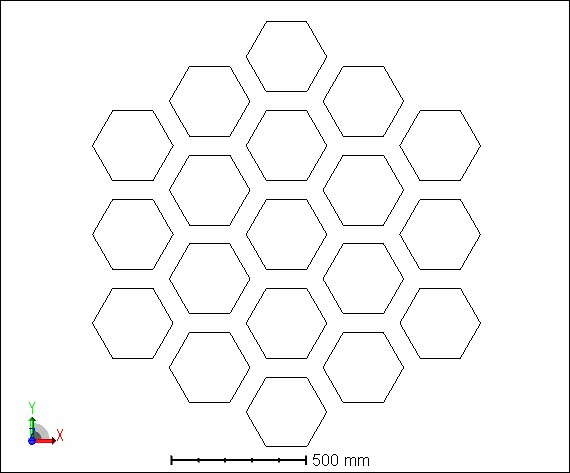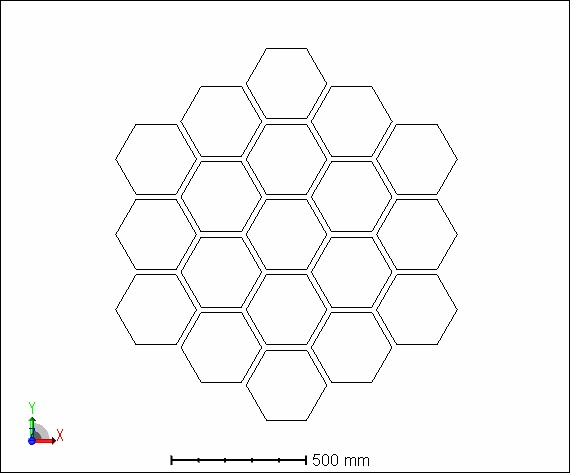
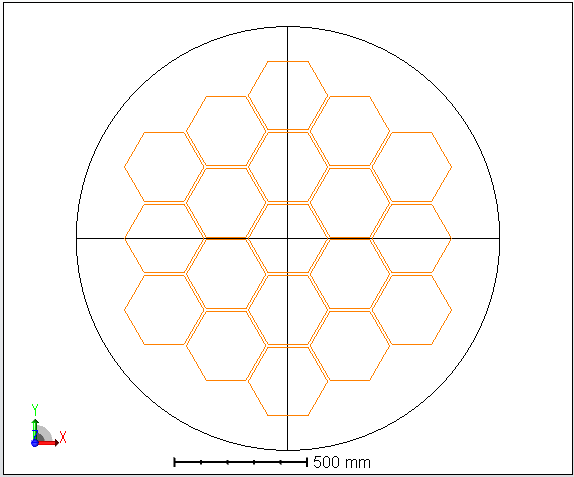
抛物反射镜面由19个子镜组成，我们将在编辑器中手动输入这些镜面。如果需要模拟数量更加庞大的反射镜组，可以使用ZPL宏来辅助系统建模。
每个子镜面与中心子镜面顶点的径向距离设置为拾取求解，使每个子镜与特定镜面的空间位置相关联。下图动画显示了在编辑器中改变其中一个子镜的位置时，其他子镜位置的整体变化。
系统使用OpticStudio产生的随机像差表示大气不均匀性对输入波前的影响。

以下为系统的部分设计指标： 镜面的矢高形状：抛物面（圆锥系数为-1）
镜面的曲率半径：-4000mm
对应焦距：-2000mm
子镜的形状：六边形
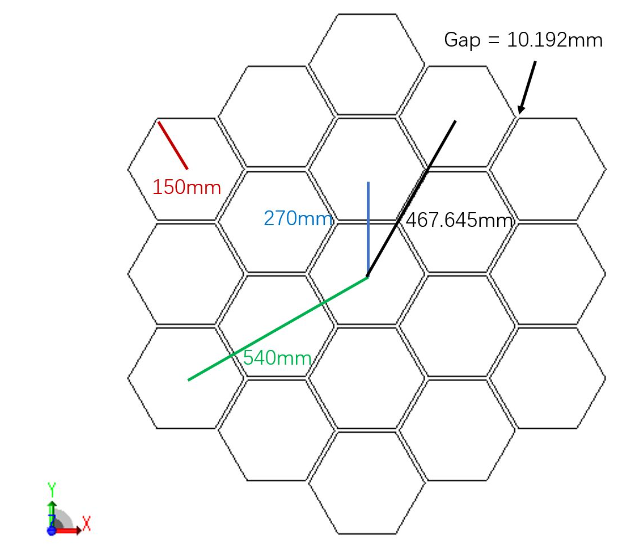
子镜的半径：150mm

在设置这些参数前，您需要充分理解多重结构、光线瞄准和系统孔径的概念。如果您对这些概念不太熟悉，请参考以下文章：

Ansys Zemax | 如何设计单透镜 第一部分：设置
Ansys Zemax | 如何使用光线瞄准?

系统的初始结构

首先进行如下系统设置：
设置系统单位为mm（系统设置 -> 单位）
设置系统波长为550μm（系统设置 -> 波长）
设置单一轴上视场X = 0, Y = 0（系统设置 -> 视场）
设置系统孔径为光阑尺寸浮动 (Float by Stop Size) （系统设置 -> 孔径）
开启光线瞄准（系统设置 -> 光线瞄准）
我们将使用多重结构功能模拟整个反射镜组，其中每个子镜使用单独一个结构建模。设置每个镜面为光阑面，并且在该表面上设置六边形的自定义孔径 (User Defined Stop Surface, UDA)。每个子光阑的偏心通过拾取求解关联在一起，并且使用光线瞄准功能使输入光线瞄准偏心的子光阑中心。下图动画展示了通过对每个子镜设置不同缩放比例的光缆位置拾取，来实现整个镜面的设置。

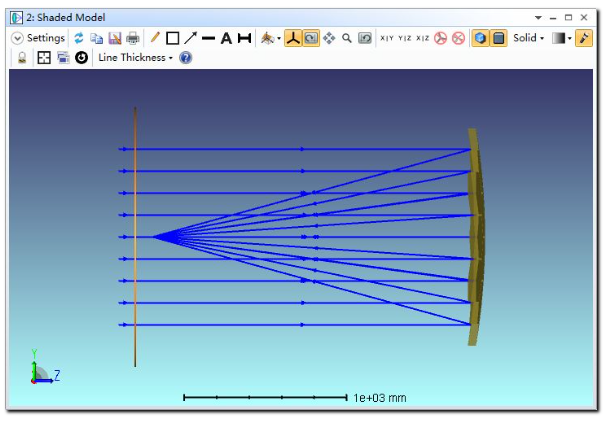
我们将在反射镜前设置一个玻璃平板，并在平板上使用公差操作数TEZI时使平板产生形变，来实现输入波前引入像差。

系统设置

设置1

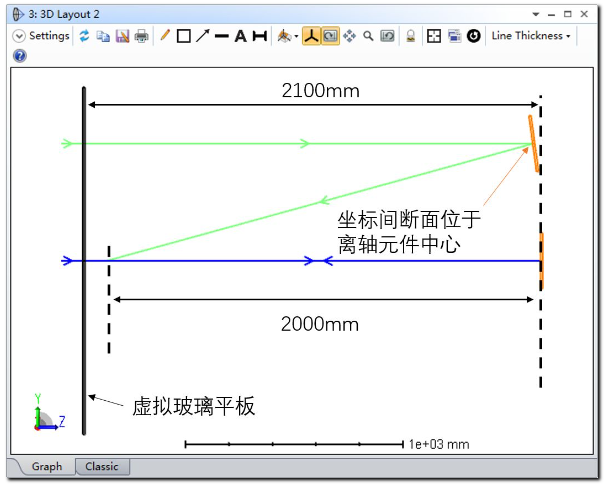
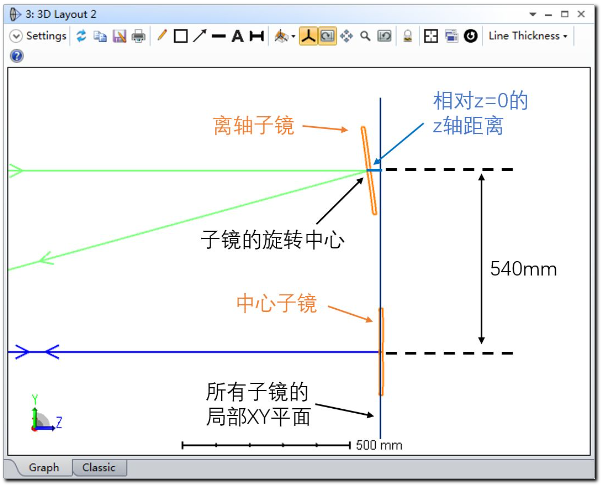
下图展示了中心子镜和其中一个偏心子镜（X = 0, Y = +540）的位置关系。需要注意的是，偏心子镜与中心子镜的相对位置关系。另外子镜的旋转中心在本系统中永远位于该表面的中心点。系统中设置有一块虚拟的玻璃平板，其折射率为常数2并且放置在像面之前100mm处。这样输入波前将在发生反射前引入像差。

设置2（透镜数据编辑器）

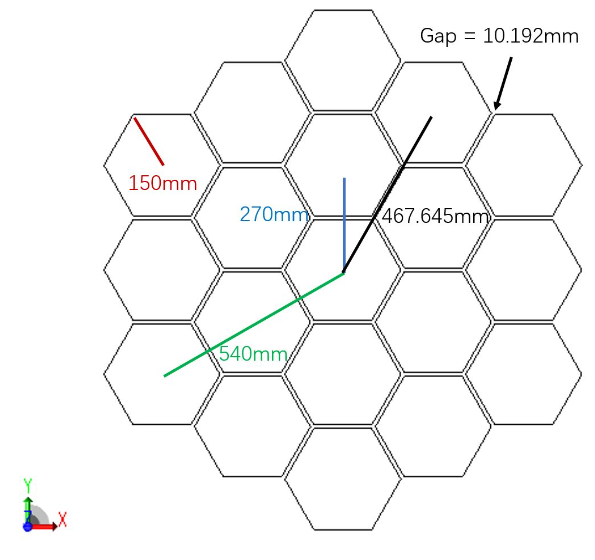
在将表面输入到编辑器之前，我们需要先创建一个用户自定义的六边形孔径，并将该孔径以 “HEXAGON.UDA” 为名保存在Zemax根目录下Objects文件夹中的Apertures文件夹中。 打开任意ASCII码编辑器。使用UDA语句 “POL” 定义六边形，其语法为： POL X中心 Y中心 半径(中心到顶点) 边数(本例中为6) 绕中心旋角(0°)

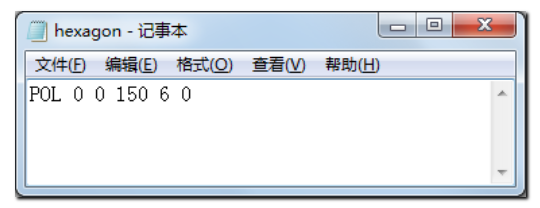
将该文本文件保存在相应文件夹下。有关UDA语法的更多信息请参考帮助系统“User Defined Apertures and Obscurations”标签。 首先，我们需要在透镜数据编辑器里对中心子镜进行建模：

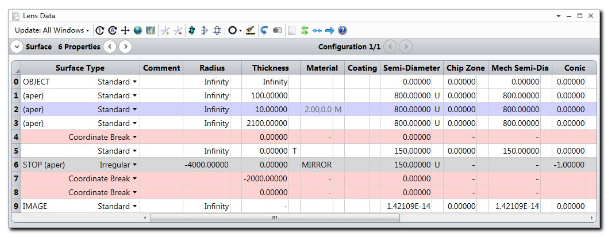
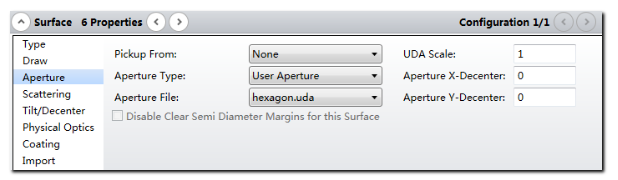
将表面6设为系统的光阑面，并将该表面的表面类型设为不规则面 (Irregular)，设置表面半径为150mm。我们使用不规则面代替标准面是因为这样可以直接使用表面的一个参数控制元件的偏心。在定义不规则面时，偏心的单位为透镜单位，倾斜的单位为度，对于中心子镜而言两参数均为零。在不规则面中定义元件倾斜和偏心的原理与使用坐标间断面定义的原理相同，但不规则面的倾斜和偏心在该光线完成该表面的光线追迹后自动复原。此段光线追迹的实际算法如下所示： 不规则面首先进行偏心，然后沿X轴倾斜再沿Y轴倾斜 系统在该表面上执行光线追迹 首先沿Y轴复原倾斜再沿X轴复原倾斜，最后复原偏心 在镜面表面6上定义自定义孔径HEXAGON.UDA：

在表面5的厚度参数上设置位置求解来保证表面3和表面5之间的总距离总是2100mm。这将确保无论设置镜片的偏心量为何值时，系统都会自动计算出正确的局部Z值。设置表面2的玻璃类型设为模型玻璃，并将折射率设为2，阿贝数及相对色散均设为0。这样设置的原因在于该平板只是用来模拟随机的相位分布：

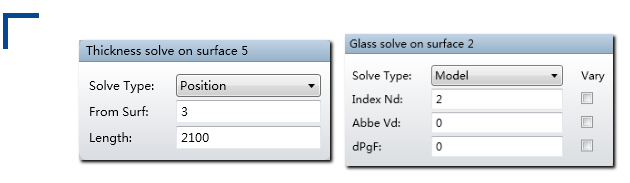
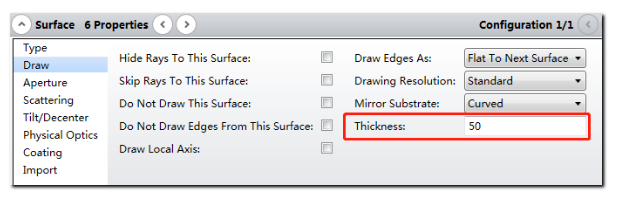
在表面属性中设置表面6镜面的基底厚度为50mm。这只会影响镜面在布局图中的绘制厚度，对其它分析没有任何影响。

设置3（透镜数据编辑器）

本文在多重结构编辑器中使用表面4坐标间断面的X方向和Y方向的偏心参数来移动光阑面位置。其中光阑面的偏心通过表面8坐标间断面的拾取求解复原。表面4坐标间断面沿X轴和Y轴的旋转角同样由表面8的拾取求解复原。需要注意的是，表面4不规则面设置的偏心需要与坐标间断面的偏心量符号相反，这样才能正确表示抛物面的离轴部分。

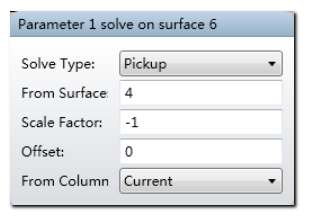
其中拾取求解的参数均设置为从表面4，缩放因子为-1。下图所示以表面6的参数2为例：

设置4（多重结构编辑器）

设置多重结构编辑器来控制表面4坐标间断面的XY倾斜和偏心（参数4/1到4/4）。同时，插入多重结构操作数THIC来控制表面3的厚度以确保离轴元件正确的Z轴距离。 当结构1的所有偏心和倾斜参数设置为0时，该结构表示中心子镜。表面3的厚度设为2100mm，这是因为中心子镜与虚拟玻璃平板的正确距离。 添加一个新的结构模拟第一块离轴子镜：

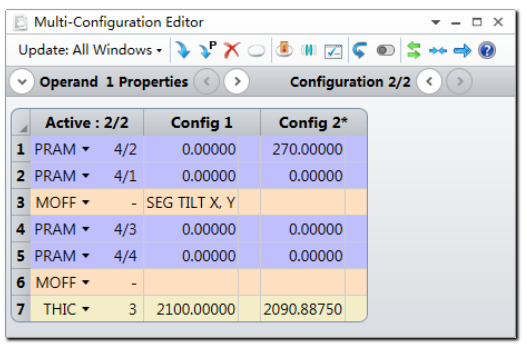
在结构2中模拟位于Y = 270mm，X = 0的离轴子镜。该子镜的中心距离虚拟平板玻璃的厚度可以通过在2100mm的基础上减去基底抛物镜在径向距离为270mm处的矢高得到。本例中不规则面的矢高计算方法与计算标准球面矢高的方法相同，其中不规则面的参数为：圆锥系数为-1，曲率半径为-4000mm以及径向坐标为270mm。可以在优化函数编辑器中使用优化操作数SSAG直接让OpticStudio计算出矢高值。

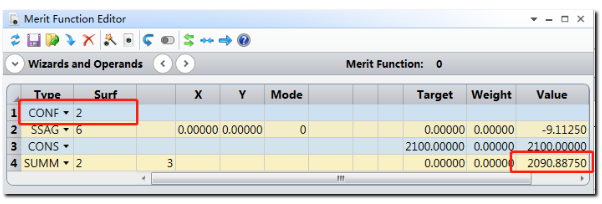
需要注意的是，此处的计算是针对结构2而言的，因此在计算操作数前需要添加CONF并设置结构为2。由于表面已经进行了偏心，因此优化操作数SSAG的参数X和Y设为0即可。其中，编辑器计算出Z轴距离2100mm - 9.113mm = 2090.887mm作为表面3的厚度需要手动输入到透镜编辑器中。 查看当前结构2的参数设置：

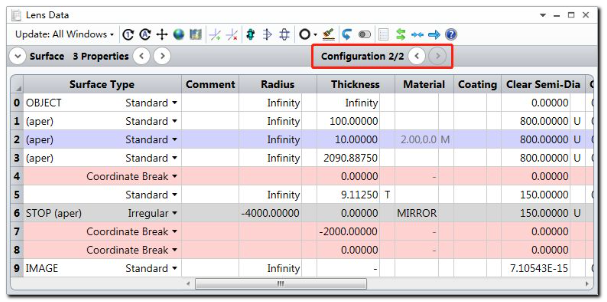
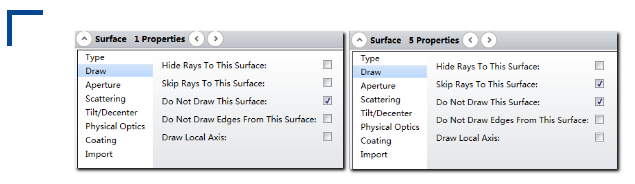
虚拟面5与表面4坐标间断面重合。因此子镜（非中心子镜）的顶点与坐标间断面的顶点在Z轴方向上相距9.113mm。也就是说，离轴抛物镜的中点与基底抛物镜的顶点及与之重合的表面4坐标间断面的顶点在Z轴方向上相距9.113mm。 由于表面5和表面1为虚拟面，因此为了使布局图正常显示，我们需要在这两个表面的表面属性的绘图选项卡中进行以下设置。

设置5（多重结构编辑器）

添加第三个结构：

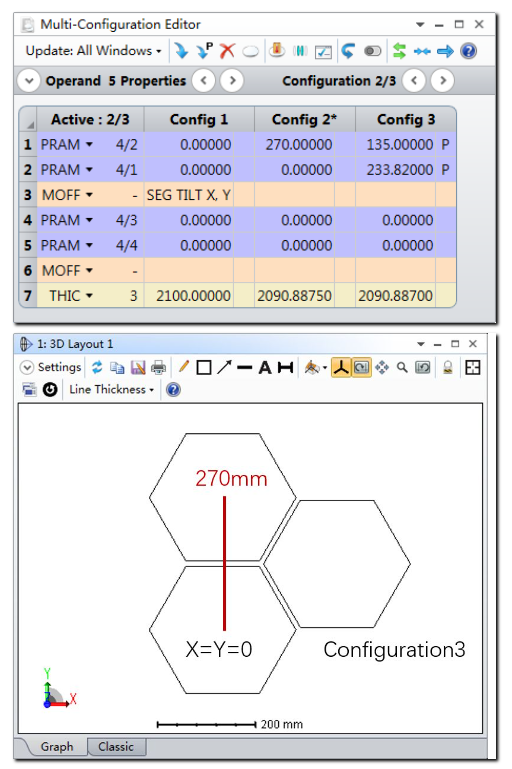
从布局图中我们可以看到，第三块子镜中点的Y方向坐标为270mm * sin(30 degree) = 270 * 0.5 mm，X方向坐标为210mm * cos(30 degree) = 270 * 0.866 mm。对于该结构下的参数1到4，我们使用拾取求解并将比例系数输入到求解类型的缩放比例中。

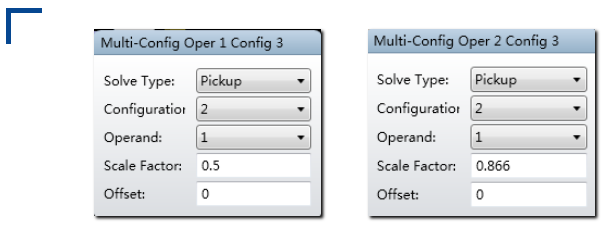
重复这一步骤至结构7：

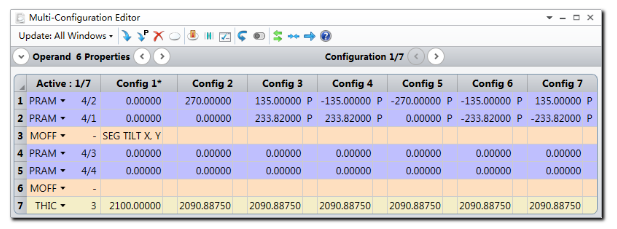
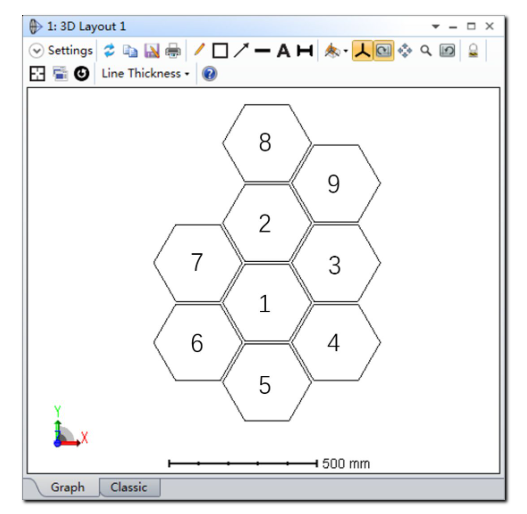
打开3D布局图，并设置如下参数：

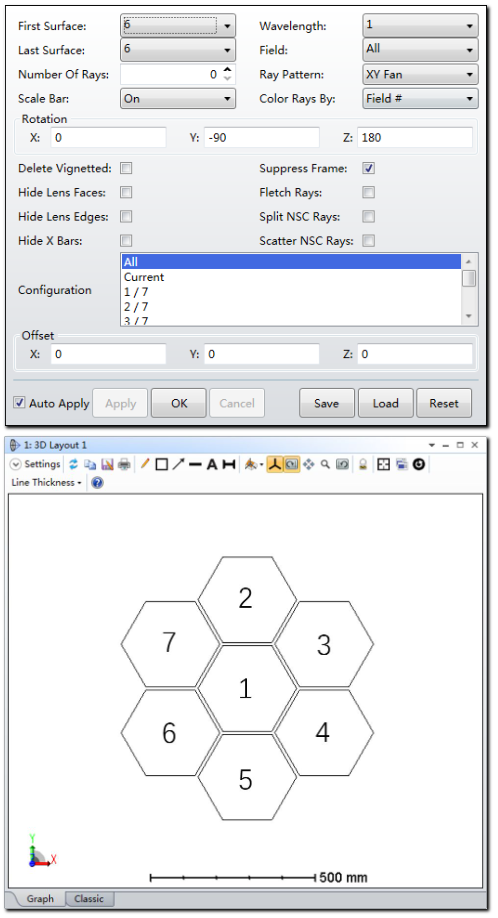
插入结构8，该结构对应的子镜中点位于X = 0, Y = 270mm * 2处。 此时表面3的多重结构操作数THIC计算结果为53.55mm。通过优化操作数SSAG计算结构8的矢高。

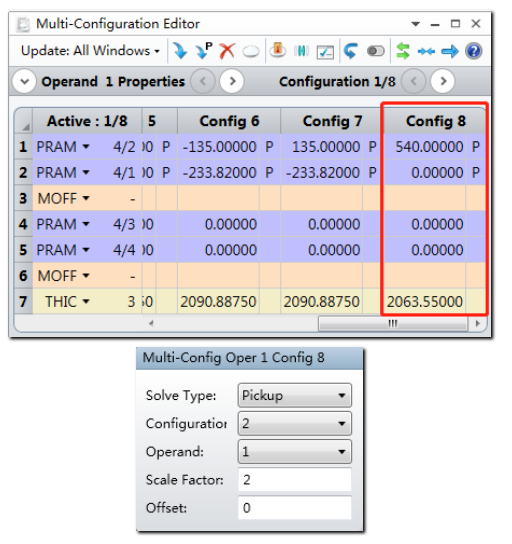
插入结构9，多重结构操作数THIC的计算结果为62.094mm并且Y轴坐标为270mm * 1.5，X轴坐标为270mm * 0.866。

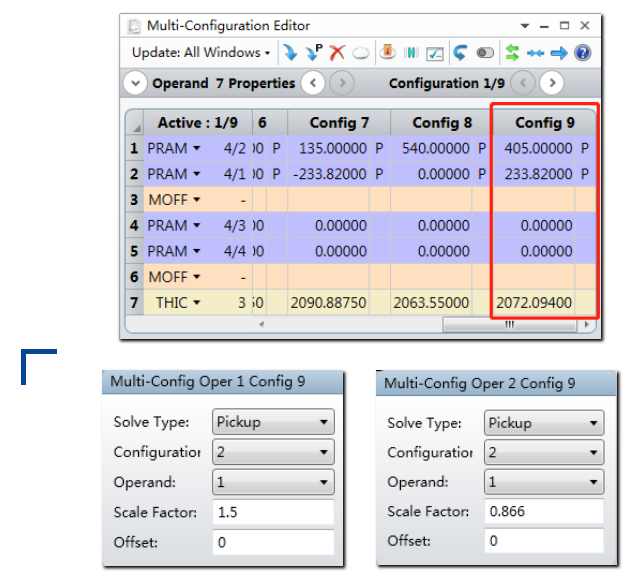
重复该步骤至结构19：

对于子镜数量更庞大的系统来说，我们可以使用ZPL宏辅助生成所有结构并设置相应的拾取求解。打开3D布局图，我们可以看到如下结构：

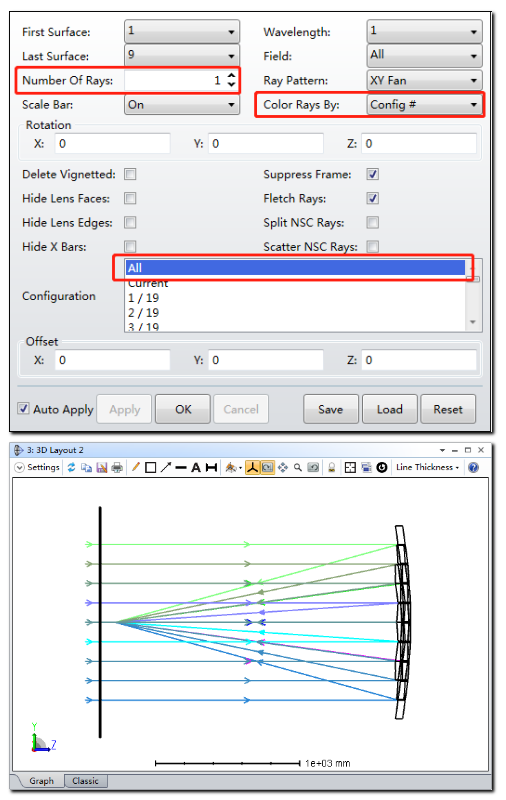
设置6（优化函数编辑器）

在设置优化函数之前，首先需要确认多重结构的拾取设置是否正确。打开优化选下卡下的滑块 (Slider) 功能，将结构2的参数1在270mm到350mm范围内进行调整。点击动画 (Animate) 将在布局图中看到如下动画效果：

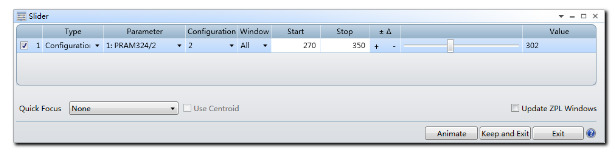
这说明系统中子镜位置的拾取求解均正确设置。点击停止 (Exit) 推出动画效果。 现在需要考虑如何设置评价函数，减小大气散射引入的像差来降低几何和衍射点扩散函数的尺寸。其中一种方法是使所有子镜在像面上光斑的几何质心位置与像面顶点重合。由于几何点扩散函数的质心和衍射点扩散函数的质心相同，因此这个方法最终会得到最小的均方根点扩散函数尺寸。此外为了使优化结果向正确的方向收敛，我们还需要限制每个子镜主光线的光程尽可能一致。 打开优化函数编辑器，利用优化函数操作数CENX和CENY（质心位置）设置所有结构在像面上光斑质心的位置为0。使用优化操作数PLEN提取所有结构主光线 (PX=0, PY=0) 的光程，并将它们限制为相同的值。对于子镜数量庞大的系统来说，可以使用ZPL宏快速设置每个结构的优化操作数。 每个结构下定义优化操作数CENX, CENY, PLEN如下所示：

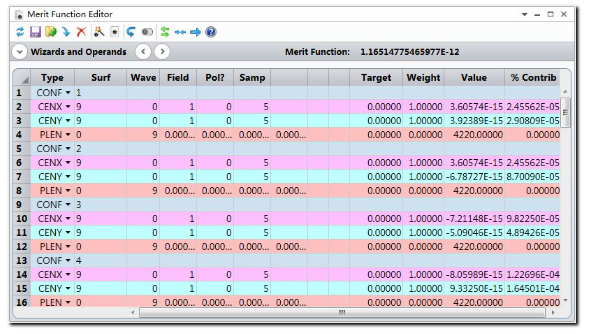
需要注意的是，此时优化操作数PLEN上未设置任何权重。这是因为系统并不需要设置主光线的光程为一个绝对值，而需要设置它们的差值为零。此处可以使用一系列权重为0的优化操作数OPVA提取每个结构的光程值，再使用权重为1的优化操作数EQUA限制一定范围内操作数相同。

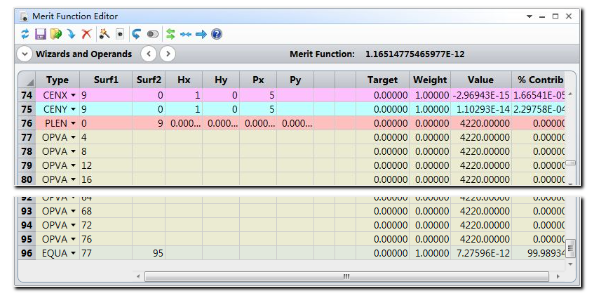
设置7（公差数据编辑器）

使用OpticStudio中的公差功能对输入波前引入随机的波前差，并通过调整每个子镜的Z轴位置和倾斜来补偿这些像差。在公差函数编辑器中使用公差操作数TEZI在虚拟玻璃平板（表面3）上引入随机的矢高差。同时，设置表面4坐标间断面沿X轴的倾斜和沿Y轴的倾斜以及镜面的位置作为优化的补偿器（变量）。 前文中使用了厚度求解来限制子镜的位置。如果想要允许子镜的位置作为优化变量，则必须在多重结构操作数中取消该求解类型并定义子镜的名义位置。在多重结构编辑器中的操作数THIC前插入一个空行，设置多重结构操作数THIC提取表面5的厚度。我们可以查看两个厚度确保玻璃平板与子镜在Z轴方向上的名义距离为2100mm。

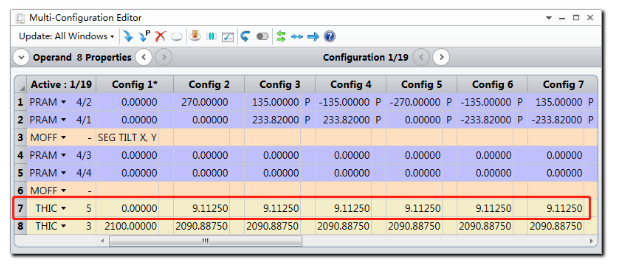
打开公差数据编辑器，插入补偿器操作数。为每个结构定义3个公差操作数CMCO分别表示X轴倾斜（多重结构第4行操作数），Y轴倾斜（多重结构第5行操作数）和Z轴位置（多重结构第7行操作数）。在定义补偿器时，必须根据多重结构编辑器中的操作数位置对补偿操作数进行分组（所有多重结构第4行操作数的补偿器为一组，依此类推）。在公差数据编辑器的最后插入公差操作数TEZI来定义引入的波前差。此处使用标准泽尼克多项式的2到9项来定义半径内波前的不规则度。其中均方根误差设置为0.5μm。

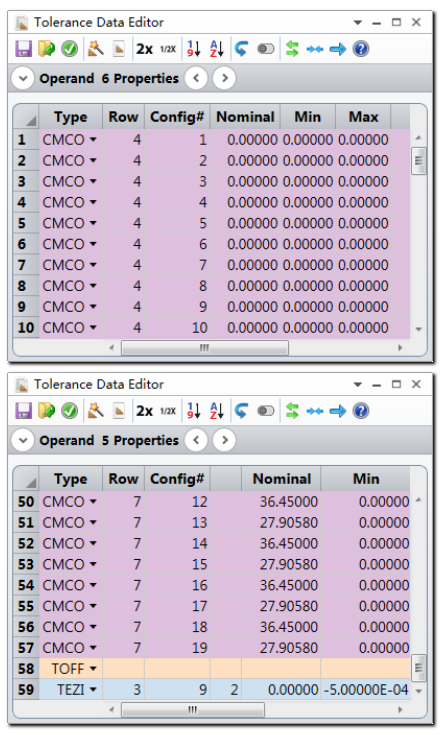
运行公差分析，并设置如下参数：

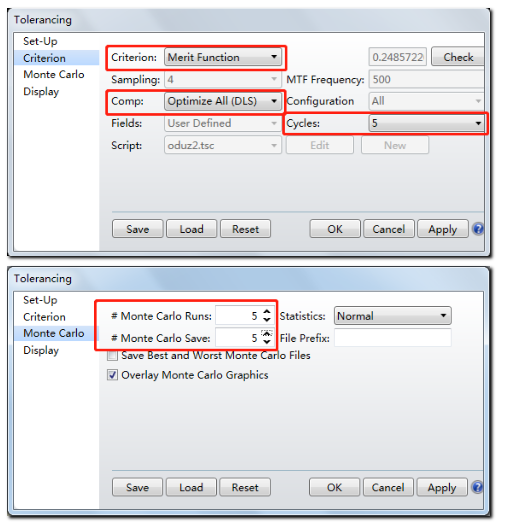
点击确定后系统提示在公差分析前取消求解设置：

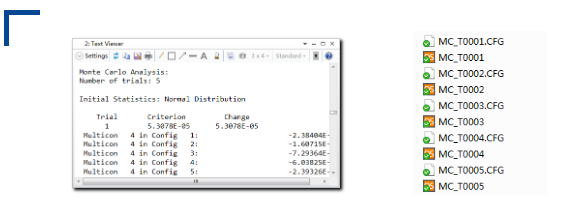
在公差分析结束后OpticStudio将打开公差报告文本窗口，并且在当前系统文件目录下保存了5个蒙特卡洛文件。

系统分析

分析1

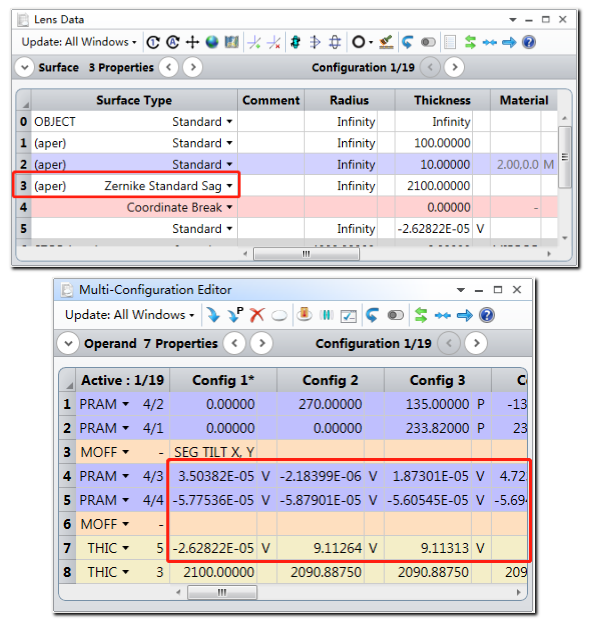
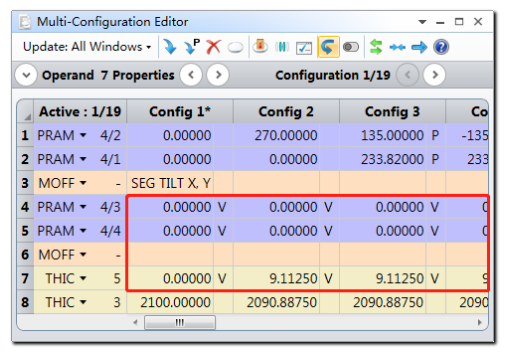
保存当前镜头文件，并打开任意一个蒙特卡洛文件。注意文件中表面3的表面类型变为了标准泽尼克多项式面，这是由于原镜头文件中的公差操作数TEZI引入的不规则度误差。并且多重结构编辑器中的所有结构的操作数4、操作数5和操作数7被设置为变量，这是因为原镜头文件中我们通过公差操作数CMCO设置这三个参数为补偿器。其中变量均不为0，这是因为在公差分析过程中改变了这些变量以使优化函数最小。

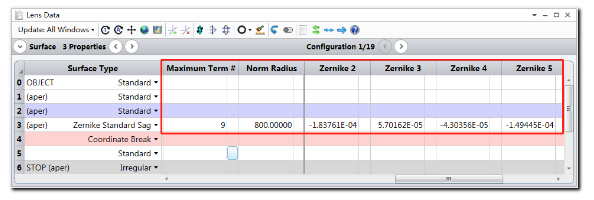
在透镜数据编辑器中，表面3的附加数据中的归一化半径被设为800mm，这与表面3在透镜数据编辑器中的半径值相等。其中第2到9项泽尼克系数则是由公差操作数TEZI随机生成的。

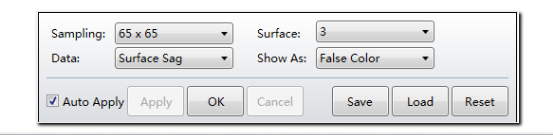
我们可以打开分析工具中的表面矢高图 (Surface Sag)，并设置如下参数来查看表面3的形状分布。下图动画显示每个蒙特卡洛文件的矢高分布。由于引入的矢高误差是随机产生的，因此在您的系统中矢高误差分布可能看起来并不相同。

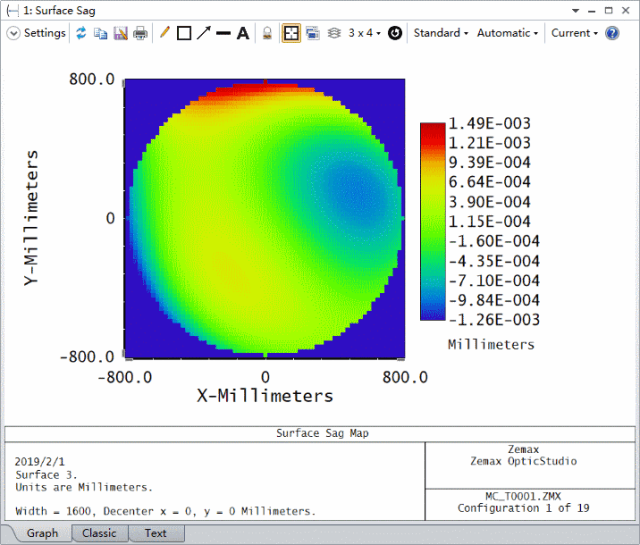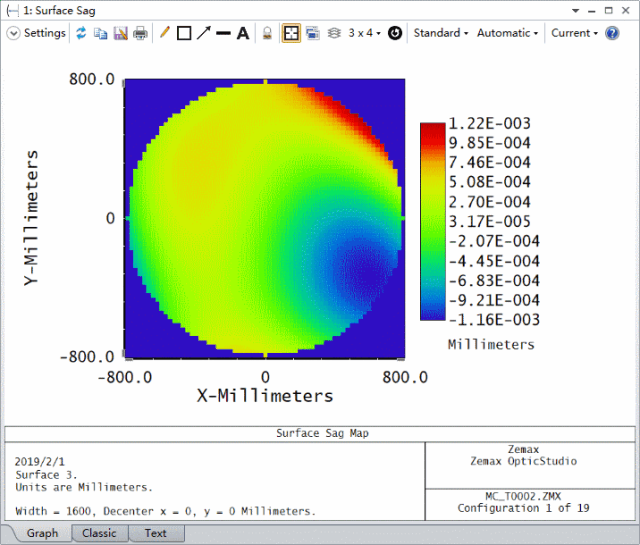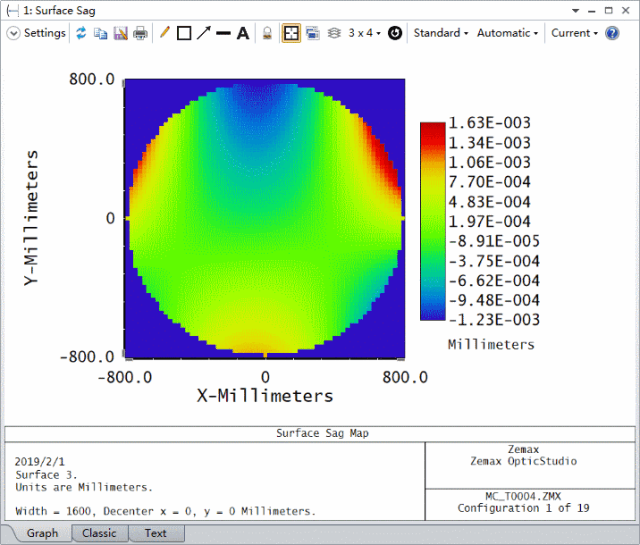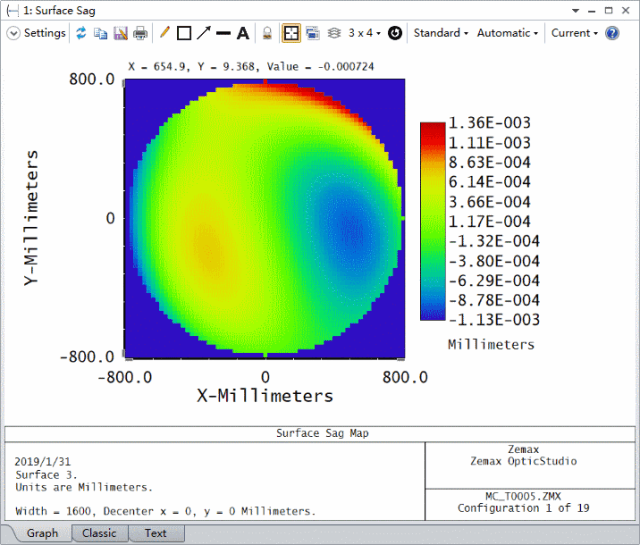
分析2

打开分析工具中的惠更斯PSF (Huygens PSF) 分析图以及标准点列图 (Standard Spot Diagram)。将分析参数设置如下，注意在窗口导航栏中选中所有结构：

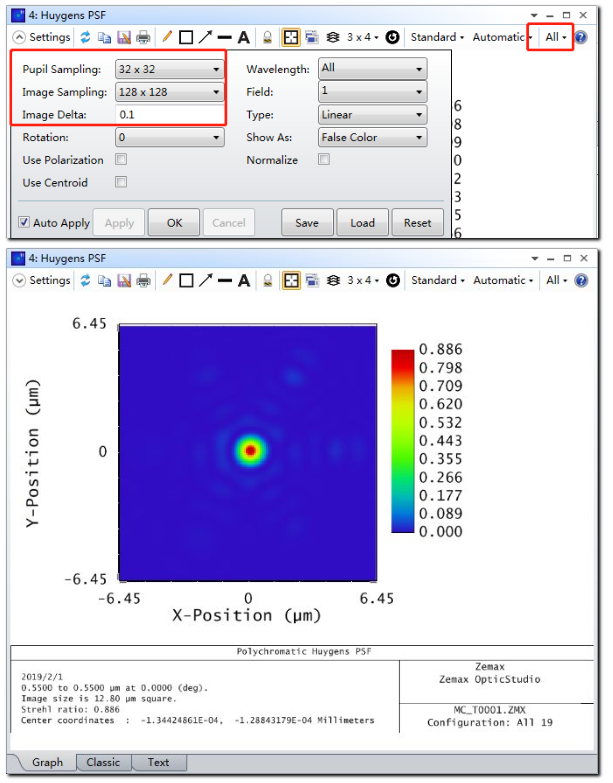
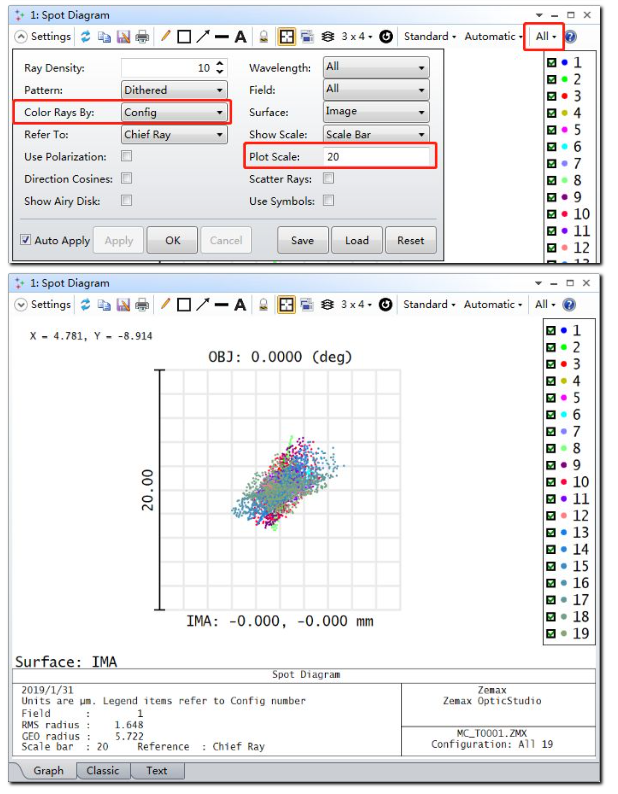
我们可以首先查看优化前的几何和衍射点扩散函数。设置多重结构编辑器中所有倾斜参数为零并复原镜面的位置：

更新分析窗口后我们将看到如下结果：

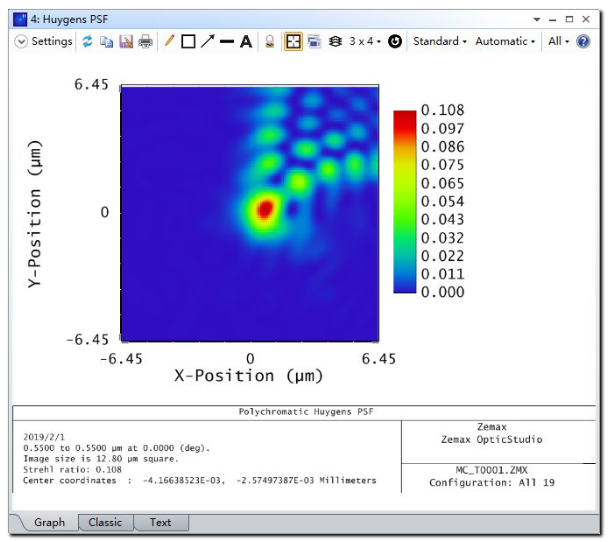
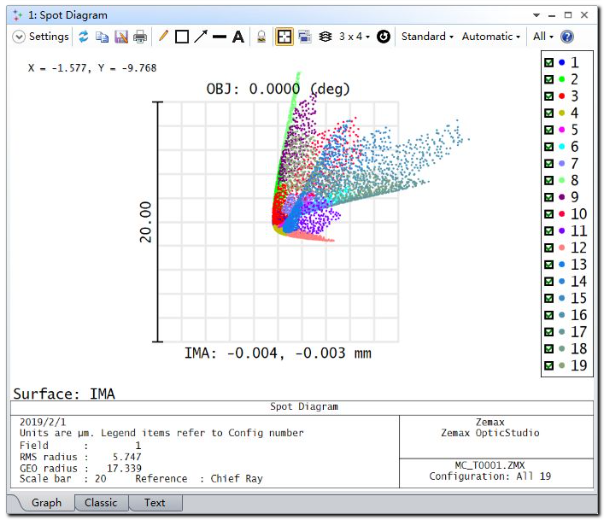
通过比较可以看出对每个子镜的倾斜和Z轴位置的调整极大的减小了像面上的像差。我们可以新建一个2x2报告图在同一窗口中查看所有分析结果。下图展示了5个蒙特卡洛文件在未进行优化时以及优化后的对比分析结果：

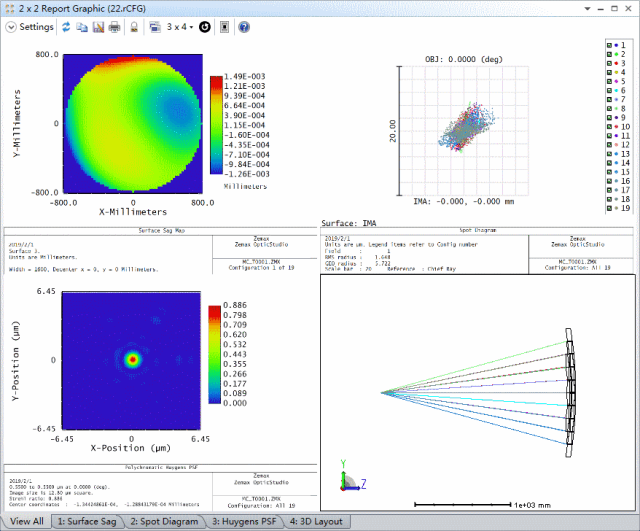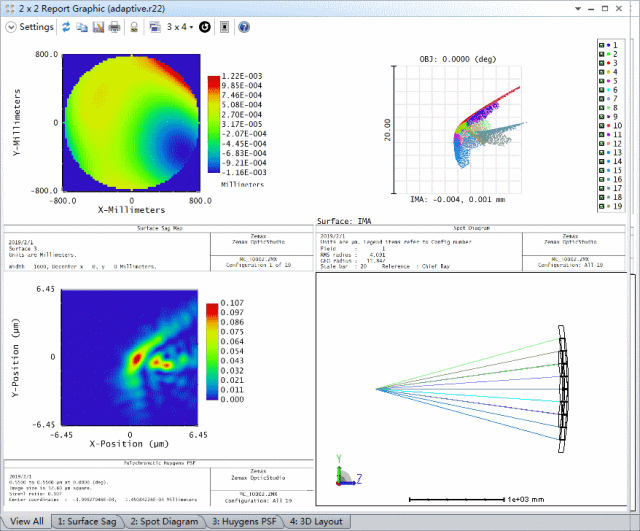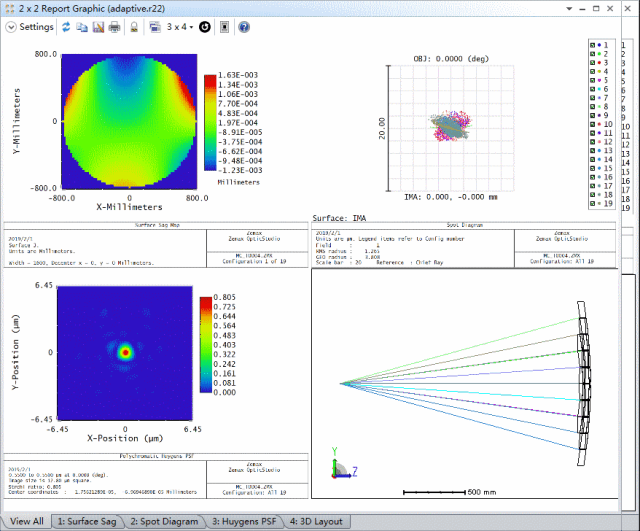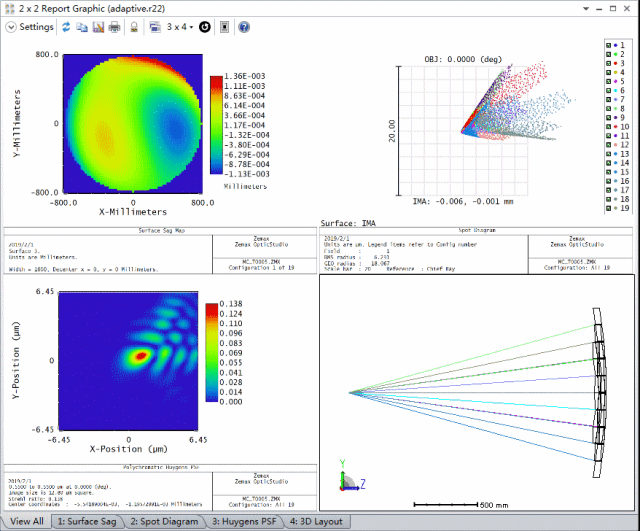
小结

这篇文章介绍了在OpticStudio的序列模式下对反射式自适应光学系统进行建模。其中主要包括以下几个要点：
每个子元件都建立在一个单独的结构中
公差功能可以用来产生随机的波前差
可以使用ZPL宏辅助完成元件数量庞大的系统建模
正确使用拾取求解可以减少系统建模的复杂性