如何在蒙特卡罗公差分析中得到扰动值?
如何在蒙特卡罗公差分析中得到扰动值?
概要
公差分析是任何光学设计的重要组成部分。这样的分析允许设计人员分析和确定系统对加工和装配过程中引入的误差的敏感度。
在Zemax OpticStudio中,可能的误差也许会被单独 (灵敏度)或同时(蒙特卡罗)引入系统。关于不同类型的公差内容,可以在Zemax OpticStudio手册中名为“公差”的的章节中找到。
Zemax OpticStudio在灵敏度分析中报告了单个参量扰动的幅度和相应系统标准的变化 (如RMS spot size) 。但Zemax OpticStudio在蒙特卡洛分析中,由于所有的扰动都是同时考虑的,因此只报告了系统标准的变化。
在大多数情况下,用户对蒙特卡罗分析时的单个扰动值不感兴趣;多数情况下,分析的目的是确定系统性能的变化,这样的分析是同时加以多个公差误差并通过统计的方式进行的。但在蒙特卡罗分析中,有时需要了解个别扰动的值,例如,当一些扰动可以用来提高系统性能时。
虽然Zemax OpticStudio在蒙特卡罗分析报告中不显示单个扰动的值,但是如果保存了蒙特卡罗文件,则该用户可以提取该信息。用户可以依次打开每个Monte Carlo文件,以确定在运行中使用的扰动。
对运行结束的大量的蒙特卡罗分析文件进行信息提取——这个过程将是冗长乏味的。但是,此过程可以使用ZPL宏来实现自动化。在本文中,我们将详细讨论如何从每个文件中提取数据,并生成每个文件中单个扰动的总结报告。
第一步:执行蒙特卡罗公差分析
从一个系统到另一个系统,公差扰动有很大的不同。因此,很难编写一个普适的ZPL宏对任何一般文件提取蒙特卡罗数据。本文开发了一个适合于特定系统进行公差分析的宏。但是,宏的总体结构可以被复制,因此可供大多数对分析文件感兴趣的用户所使用。
创建宏的第一步是确定在系统中如何计算公差扰动。本文使用的示例是Cooke triplet(在示例文件路径\Samples\Sequential\Objectives\Cooke 40 degree field.zmx)。在分析中使用默认的公差设置:
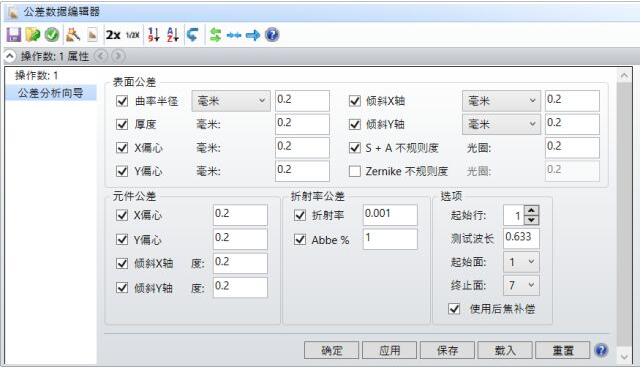
对默认设置进行微小改变,即:a. 关闭中间厚度补偿 (调整=所有面的TTHI操作数) b. 表面偏心参考每个镜头的背面(删除表面2,4,6所有TSDX和TSDY操作数),由此产生的系统可在存档文件(.ZAR)中找到。
本系统有41个扰动要分析:
☆ 6个曲率半径。
☆ 5个厚度(使用后焦补偿器)
☆ 3个元件X偏心。
☆ 3个元件y偏心。
☆ 3个元件X倾斜。
☆ 3元素对Y倾斜。
☆ 3个表面X偏心。
☆ 3个表面Y偏心。
☆ 6个表面不规则度
☆ 3个折射率
☆ 3个阿贝数
对应于公差数据编辑器中的41个公差操作数。因此,我们编写的宏将用来存储所有蒙特卡罗运行中的41个扰动数据,然后进行蒙特卡罗分析。在本例中,选择RMS光斑半径作为公差分析标准:
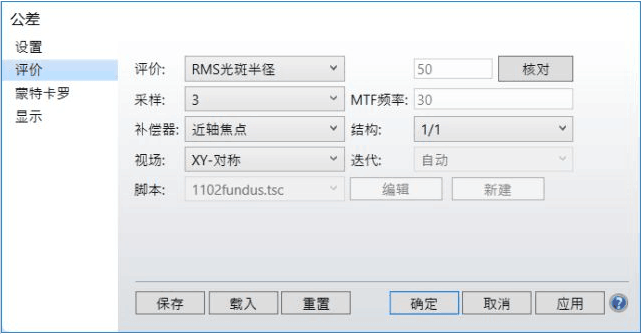
并进行了100次蒙特卡罗分析:
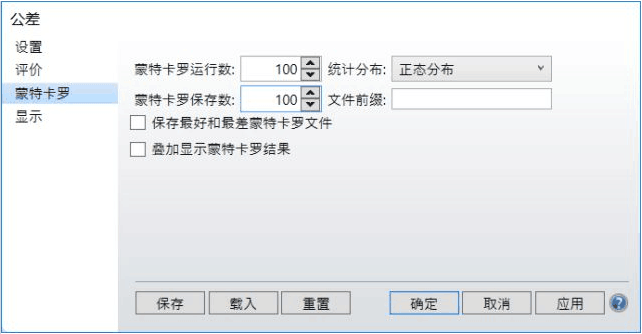
值得注意的是,为了提取所需的数据,我们必须保存每次运行,文件的名称是“MC_Txxxx”,其中xxxx对应于运行次数。
第二步:创建ZPL宏
本文最后将提供用于从蒙特卡罗中提取数据的ZPL宏。第一步是指定执行的运行次数:
! Define number of MC runs
n_files = 100
然后定义数组来存储每次运行的扰动值。创建数组来保存6个曲率半径值(trad6_per trad1_per,…),5个厚度值(tthi1_per,…,tthi5_per)等。对于使用操作数TIRR定义的表面不规则度,创建数组来存储不规则度大小(tirrm1_per,…,tirrm6_per)以及像散误差角(tirra6_per tirra1_per,…)。还定义了一个数组来保存每此运行的标准值(tcrit_per)。然后利用TOLV函数获得每个扰动(半径、厚度等)的名义值:
! Get nominal values for radii, thicknesses, indices, and Abbe numbers
! (all other perturbations have a nominal value of zero)
trad1_nom = TOLV(3,90)
trad2_nom = TOLV(4,90)
trad3_nom = TOLV(5,90)
trad4_nom = TOLV(6,90)
trad5_nom = TOLV(7,90)
trad6_nom = TOLV(8,90)
tthi1_nom = TOLV(9,90)
tthi2_nom = TOLV(10,90)
tthi3_nom = TOLV(11,90)
tthi4_nom = TOLV(12,90)
tthi5_nom = TOLV(13,90)
tind1_nom = TOLV(38,90)
tind3_nom = TOLV(39,90)
tind5_nom = TOLV(40,90)
tabb1_nom = TOLV(41,90)
tabb3_nom = TOLV(42,90)
tabb5_nom = TOLV(43,90)
如ZPL宏中注释所示,在本例中,未列出的扰动(如元件倾斜)的名义值均为零。
接下来,我们将遍历所有蒙特卡罗文件并提取所需的扰动数据。首先为名义文件获取完整的文件名,以便在循环结束时重新加载这个文件:
N$ = $FILEPATH()
然后定义一个字符串变量,它将是蒙特卡罗文件名的基础(包含完整的路径——假设所有的蒙特卡罗文件都在同一目录下):
A$ = $PATHNAME()
B$ = A$+"\MC_T"
然后使用FORMAT关键字指定文件编号格式,该编号将被添加到文件名中,以便与Zemax文件编号系统保持一致:
FORMAT "%#04i" LIT
这个关键字只适用于Monte Carlo文件的数量< 10,000,这也貌似是我们所执行分析类型的合理限制。最后,开始FOR循环:
FOR i, 1, n_files, 1
在该循环中,可生成一个字符串,此字符串将包含蒙特卡罗文件的完整文件名,然后使用LOADLENS关键字加载文件:
F$ = B$+$STR(i)+".zmx"
LOADLENS F$
然后从文件中提取所需的数据,使用以下函数提取相应的值,MFCN函数(公差分析标准值),RADI函数(曲率半径),THIC函数(厚度),及PARM函数(表面和元件偏心,元件倾斜,表面不规则度),SOLV函数(折射率和阿贝数)。在一些的情况下,为了计算扰动值,需要从得到的值中减去名义值。
可以看到,在宏中输入的表面数目(surface number)已被硬连接到代码中,并且在所有情况下,表面数目与名义文件中的表面数目不同。这是由于在模拟元件倾斜和偏心时通过坐标断点面引入了更多的面,因此蒙特卡罗文件相对于名义文件会有额外的表面。为了确定每种情况下的合适的表面数字,可手动打开并研究一个蒙特卡罗文件。
完成FOR循环后,重新加载名义文件。并使用另一个FOR循环将结果打印到屏幕上,同时使用FORMAT关键字来控制打印数据的数值精度:
! Print the results
PRINT "Run# Criterion ",
PRINT "RAD1 RAD2 RAD3 RAD4 RAD5 RAD6 ",
PRINT "THI1 THI2 THI3 THI4 THI5 ",
PRINT "TEDX12 TEDY12 TETX12 TETY12 ",
PRINT "TEDX34 TEDY34 TETX34 TETY34 ",
PRINT "TEDX56 TEDY56 TETX56 TETY56 ",
PRINT "TSDX1 TSDX3 TSDX5 TSDY1 TSDY3 TSDY5 ",
PRINT "TIRRM1 TIRRM2 TIRRM3 ",
PRINT "TIRRM4 TIRRM5 TIRRM6 ",
PRINT "TIRRA1 TIRRA2 TIRRA3 TIRRA4 TIRRA5 TIRRA6 ",
PRINT "TIND1 TIND3 TIND5 ",
PRINT "TABB1 TABB3 TABB5"
FOR i, 1, n_files, 1
FORMAT "%#04i" LIT
PRINT i, " ",
FORMAT 10.5 EXP
PRINT tcrit_per(i), " ",
FORMAT 10.5
PRINT trad1_per(i), " ", trad2_per(i), " ", trad3_per(i), " ",
PRINT trad4_per(i), " ", trad5_per(i), " ", trad6_per(i), " ",
PRINT tthi1_per(i), " ", tthi2_per(i), " ", tthi3_per(i), " ",
PRINT tthi4_per(i), " ", tthi5_per(i), " ",
PRINT tedx12_per(i), " ", tedy12_per(i), " ",
PRINT tetx12_per(i), " ", tety12_per(i), " ",
PRINT tedx34_per(i), " ", tedy34_per(i), " ",
PRINT tetx34_per(i), " ", tety34_per(i), " ",
PRINT tedx56_per(i), " ", tedy56_per(i), " ",
PRINT tetx56_per(i), " ", tety56_per(i), " ",
PRINT tsdx1_per(i), " ", tsdx3_per(i), " ", tsdx5_per(i), " ",
PRINT tsdy1_per(i), " ", tsdy3_per(i), " ", tsdy5_per(i), " ",
FORMAT "%+10.5e" LIT
PRINT tirrm1_per(i), " ", tirrm2_per(i), " ", tirrm3_per(i), " ",
PRINT tirrm4_per(i), " ", tirrm5_per(i), " ", tirrm6_per(i), " ",
FORMAT 10.5
PRINT tirra1_per(i), " ", tirra2_per(i), " ", tirra3_per(i), " ",
PRINT tirra4_per(i), " ", tirra5_per(i), " ", tirra6_per(i), " ",
PRINT tind1_per(i), " ", tind3_per(i), " ", tind5_per(i), " ",
PRINT tabb1_per(i), " ", tabb3_per(i), " ", tabb5_per(i), " "
NEXT i
最后,使用RELEASE关键字释放与每个数组关联的内存。
此宏虽是为特定的示例文件提供的定制ZPL。但即使文件或公差分析中的扰动不同,宏的基本结构框架可能仍然保持不变。
第三步:运行宏
完成宏编写后,就可以运行并生成所需的数据:

总结
一般来说,设计者对由蒙特卡罗公差分析产生的单个扰动不感兴趣。但如果保存所有的蒙特卡罗文件,那么文件中的信息是可以获得的。可通过ZPL宏来自动提取所需数据。点击另存为可将结果输出为文本文件进行其他分析。

