概述

这篇文章介绍了当光源入射到系统入瞳时，“切趾(Apodization)”是如何对光源辐照度分布进行定义的。本文所用的示例文件请从以下链接下载：

介绍

在维基百科中，“切趾(Apodization)”的字面意思为“去脚化(Removing the foot)”。其实际作用为对数学函数、电信号、光线传播或机械结构的形状进行改变，进而去除或平滑边缘的不连续性。在光学设计中，我们使用切趾来改变光学系统入射光的强度分布或系统的透过率分布，并且它可以用来描述复杂的分布特征。在光学设计中，切趾也经常称作“变迹”。

在OpticStudio中我们使用切趾来描述光学系统的非均匀辐照度特性。我们将通过示例文件进行详细介绍。在示例系统中，近轴透镜用来表示一个成像质量接近衍射极限的光学系统，可以看到入射光在整个光瞳上的强度分布是均匀的，如下图所示：

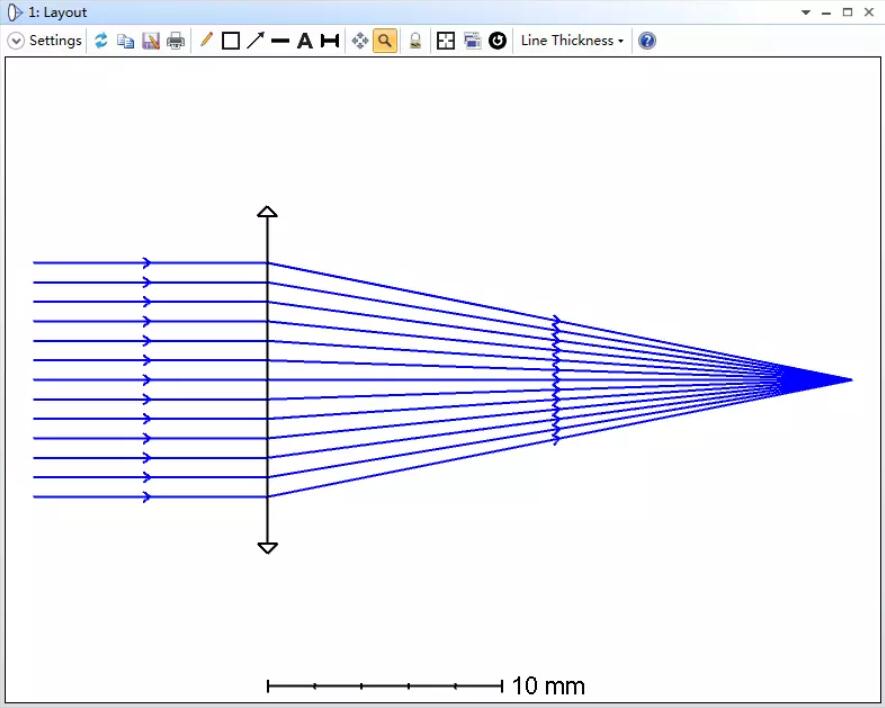
打开FFT点扩散函数分析功能，通过其结果可以看到汇聚光斑的强度分布由于衍射效应而呈现出经典的艾里斑形状。这也符合平顶函数的傅里叶变换为贝塞尔函数的事实。

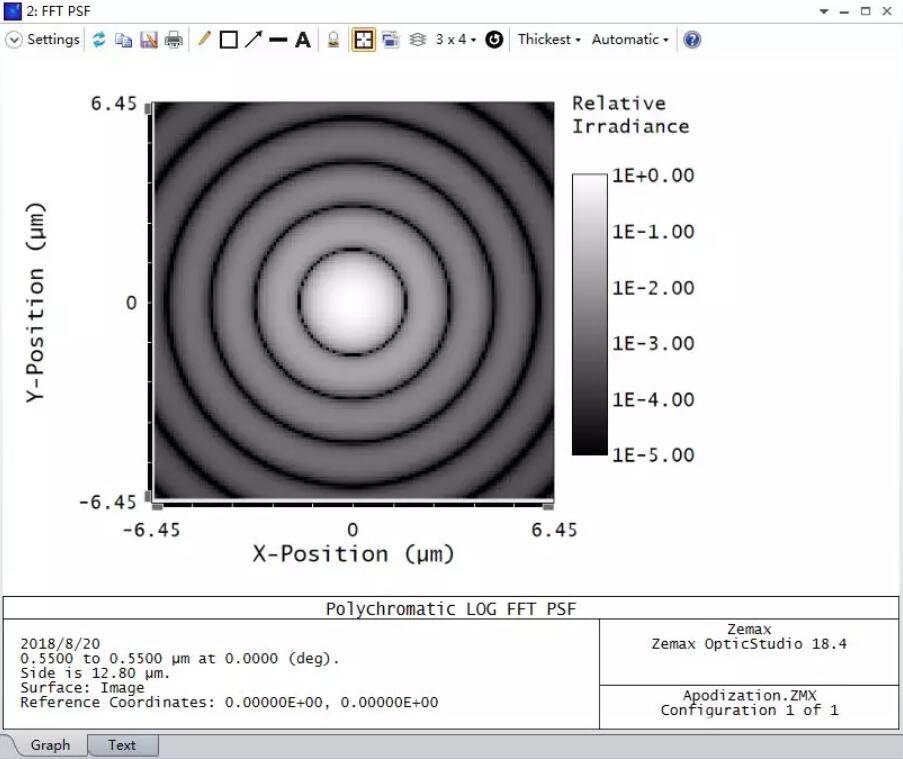
需要注意的是，为了更显著的展示衍射图案，该分析结果的强度比例尺为对数坐标。并且像面采样间距设为0.1。

如果这时我们使用高斯分布的入射光取代之前的均匀分布的平顶入射光，进而改变入射光在光瞳上的强度分布，如下图所示：

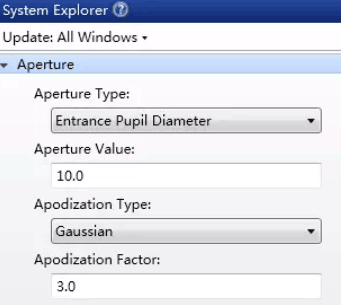
在本例中，我们使用切趾类型为“高斯型(Gaussian)”，切趾因数为3。这将使入射光的强度分布变为高斯分布，并且归一化光瞳半径为1处的光强为光瞳中心强度的1/e2的三次方根，此时系统的布局图如下所示：

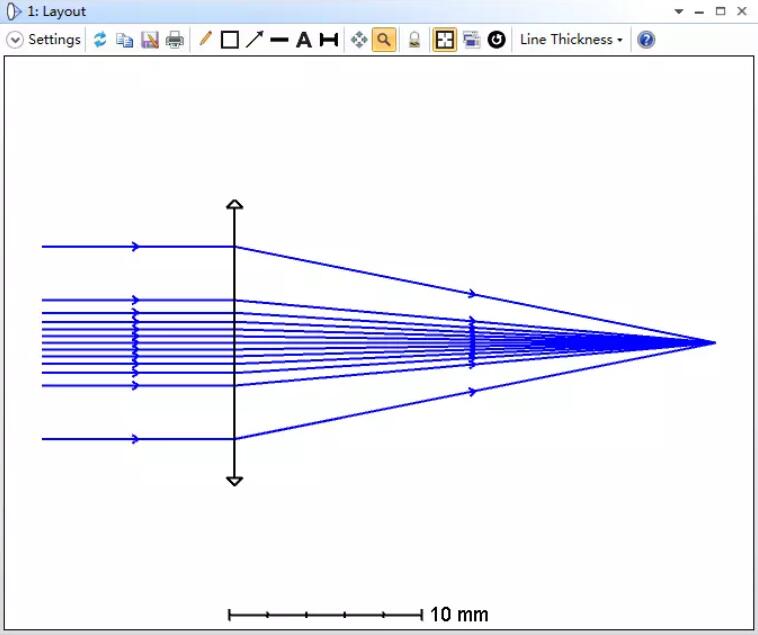
现在入射光相对来说只有很小一部分的能量被系统光阑拦截掉，并且由于高斯函数的傅里叶变换仍为高斯函数，因此FFT PSF分析结果如下图所示：

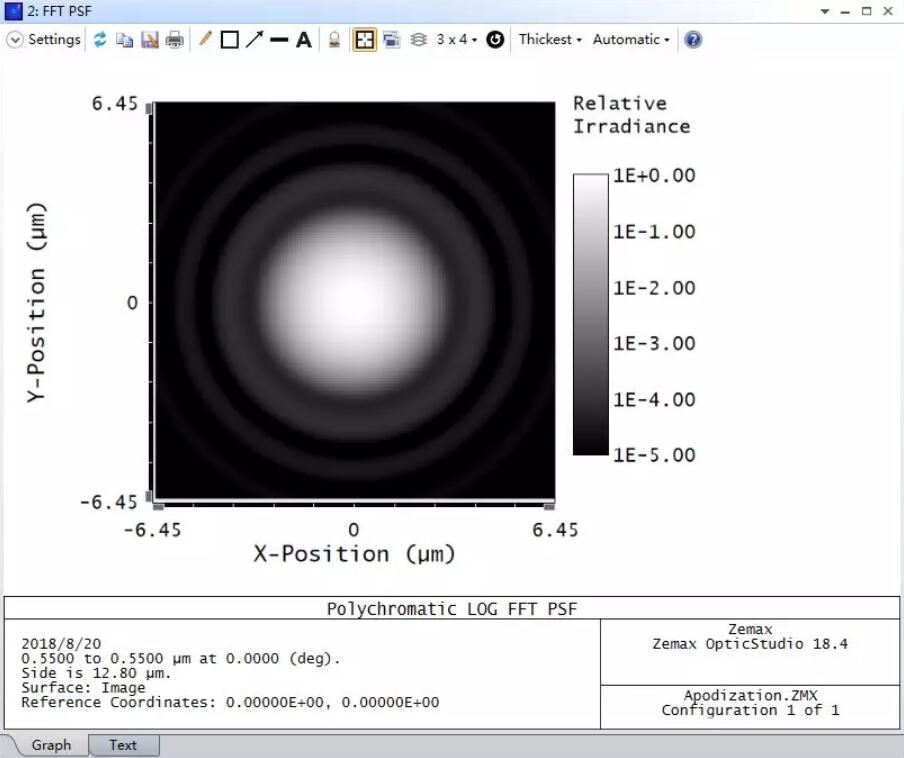
正如切趾的字面意思一样，我们通过设置切趾类型和切趾因子去掉了光强分布的“脚部”，也就是衍射图案的边缘外环部分。需要注意的是，此时的透镜组并没有发生改变，只是将强度分布由均匀分布改变为以光瞳半径为自变量的函数。在本例中，孔径边缘只有少部分能量，因此只有少部分能量从中心衍射到外部。

切趾一词也同样用于空间滤波器中。例如使用小孔光阑，将艾里斑周围的衍射环滤除，使光斑中心部分通过小孔。以此来实现对光斑的“去脚化”。但是在光学设计的术语中，切趾的应用范围更加广泛，它用来描述光瞳上任意的辐照度分布函数，无论系统的衍射光斑是否只有一个主峰。

切趾类型

OpticStudio支持多种切趾类型：

均匀 (Uniform)：在该类型下，光线在整个入瞳上是均匀分布来模拟均匀照明的情况。系统中物体处于较远距离时一般属于这类情况。

高斯 (Gaussian)：光的振幅随光瞳的半径变化而变化，并其其强度呈高斯型分布。并且，切趾因子用来描述振幅随光瞳半径增大而减小的程度。振幅和光瞳半径的关系为：

其中A为振幅，ρ为归一化光瞳半径，G为切趾因子。当G为0时，振幅在整个光瞳上为均匀分布。当G为1时，光束的振幅在光瞳边缘处下降为1/e，也就是说光强下降到1/e2，约为峰值光强的13.5%。

余弦立方 (Cosine Cubed)：该类型模拟点光源照明一个平面时的光强分布情况。当该平面为入瞳时，请您确保只有在点光源或视场点靠近光轴的情况下使用这一切趾类型。我们使用“余弦立方”这一词是因为对于一个点光源来说，光束照明的平面上光强和角度的关系为：

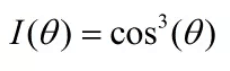
其中θ为Z轴与入射到入瞳上的光线间的夹角，在光瞳中心处的相对光强为1。

OpticStudio还支持在任意面上用户自定义切趾函数，而不只是在入瞳上定义。有关用户自定义表面切趾DLL的详细信息，您可以在帮助系统中的 “The Setup Tab > Editors Group (Setup Tab) > Lens Data Editor > Sequential Surfaces (lens data editor) > User Defined” 中查看详细信息。

您可以使用透过率在任意表面定义切趾。在DLL中，透过率函数可以是基于光线坐标、方向余弦、表面参数或其他数据的任意公式，或通过表中数据以及其他DLL中可使用的方法来定义。