Ansys Zemax | 利用 TrueFreeForm 面进行网格自由曲面的优化

在这篇文章中，我们将演示如何使用 OpticStudio 的 TrueFreeForm 面，设计AR/VR设备中的人眼追迹系统（eye-tracking subsystem），这个系统通常位于装置的楔形透镜结构中。此外，为了完成子孔径（sub-aperture）矢高（sag）的优化，我们会透过优化 TrueFreeForm 面的网格矢高（grid-based sag）以达成目标。在优化的过程中，人眼追迹系统的影像质量可以随之提升。

简介

在 OpticStudio 中，TrueFreeForm 面属于序列模式下的一种面型。此表面结合了多项式（Polynomial）和网格矢高两种面型的特性。另外，以 TrueFreeForm 面进行设计时，我们还可以对网格矢高中的每个点为目标，并且以非参数化（non-parameterized）的方式进行矢高的优化。当用户想以局部区域为优化目标，或是多项式函数无法完整呈现矢高架构时，TrueFreeForm 面会是我们的好选择。

背景知识

在使用 TrueFreeForm 面进行设计时，我们能以多项式函数的型式，如双锥 toroidal （biconic toroidal）、偶次项非球面（even asphere）、Zernike标准矢高（Zernike standard polynomial）、扩展多项式（extended polynomial）以及网格矢高定义的方式设定矢高。在同一个表面取得上述的函数可以为我们的设计过程来一些好处，例如原先以扩展多项式（extended polynomial）、双锥 toroidal （biconic toroidal）或网格定义（grid-based definitions）为目标进行的自由曲面优化，现在可用Zernike系数对不规则的设计进行额外的公差分析。此外，我们还可以将网格矢高上的各点设为变量进行矢高的优化，这是以TrueFreeForm面进行设计时较有趣的一点。

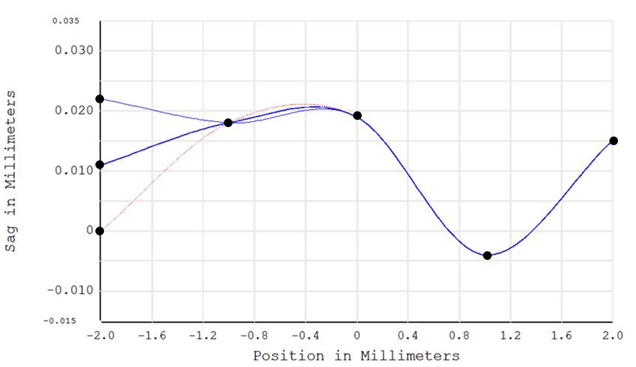
相较于参数式（parametric）优化，网格矢高优化具有许多优点。由于预设的网格矢高内插算法是以双三次样条（bicubic spline）的方式进行计算，因此值域中的每个点只会对网格中相邻的至多两点产生影响。假如我们针对数据中的一点进行优化，则系统只会改变局部的表面结构，距离较远的表面信息则会维持原样。下图显示了一个简化的一维平滑曲线模型。图中的三条曲线分别以5个点定义出三次样条（cubic spline）。我们可以看到图中最左边的点会在三条曲线间移动，但只会对距离最近的两点产生影响。

接着我们利用下图将上述概念推广到二维空间。我们先以二维网格的矢高值表示目标的表面结构，并选择其中一点进行矢高的优化（图中红点），可以看到只有蓝色方形（5x5个点）内的区域会受到影响。

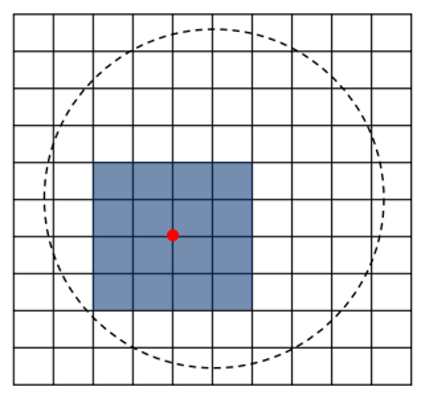
以上的例子告诉我们两件事。第一，以网格矢高的方式进行优化，我们可以将优化目标限制在局部的区域中; 相对的，使用参数式优化时，每当我们对单一数值进行变更，则整个表面的结构均会发生变化。第二，我们可以较轻易的产生特殊的表面几何关系，而这是我们很难以有限次的多项式函数达成的。

在使用网格矢高优化时有两点需要特别注意。由于矢高网格会运用到三次方的内插法（cubic interpolation），这代表由一组数据点所产生的曲线会受到几何关系的限制。此外，用于定义网格的矢高数据量也是进行优化时重要的考量。资料点太多会降低优化的效率（变数过多），且会对取样产生负面的影响（在接下来的篇幅中会再详述）。另一方面，若系统以过少的数据点进行优化，将难以产生最佳的优化表面。因此，在使用网格矢高的方式进行优化前，我们需要更谨慎的设定网格的参数。

实际案例-TrueFreeForm 面网格优化

设置

在这个范例中，我们利用将以一个具有自由曲面楔形棱镜的头戴式透视显示器（optical see-through head mounted display）进行设计，此光学系统参考了Gao C. 和Hua H.的专利（EP3270194A1）。显示器中的NIR（近红外光）人眼追迹系统包含了三个相同的光学表面，和一个用于聚焦的楔形单透镜。一开始，我们以扩展多项式（extended polynomial）的方式在OpticStudio中建立三个面。由于TrueFreeForm面也能支持扩展多项式函数，所以可以此作为设计的起点。接着，我们将进行微显示器的优化和人眼追迹系统的嵌入。在这些过程中，我们还不会对参数式自由曲面的光学表面进行校正。

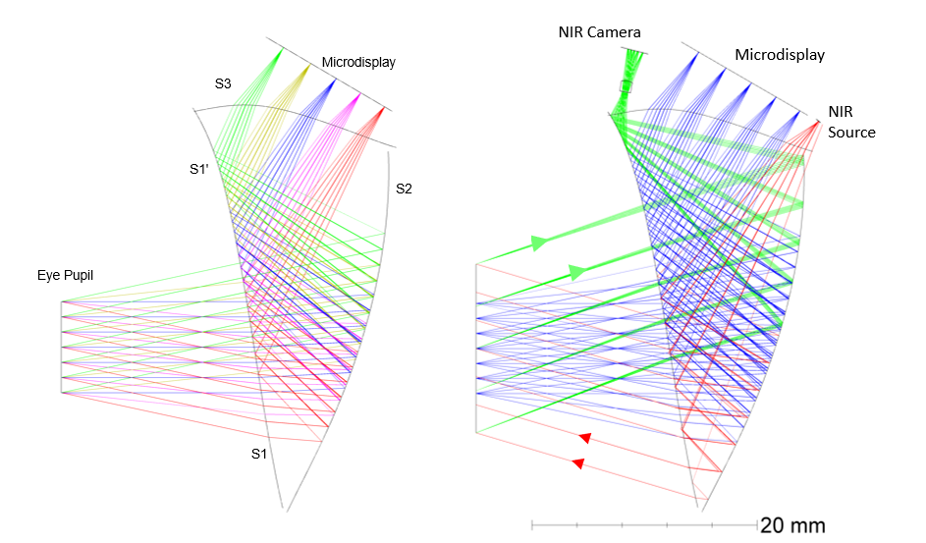
注意，为了简化设计我们忽略了光学系统中的透视（see-through）结构，并且只以单一波长的入射光进行优化。

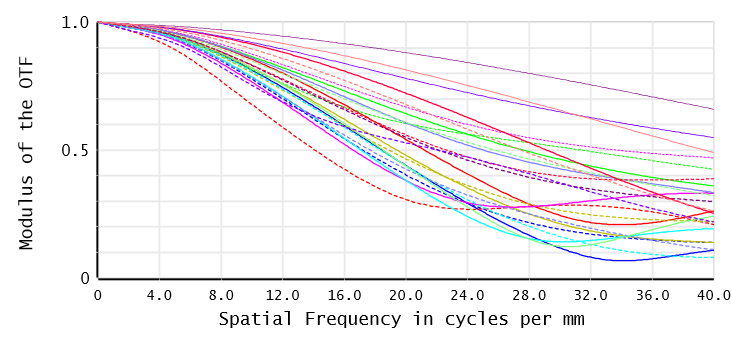
此外，一开始的光学表面优化是以显示器系统的成像为目标，而忽略了人眼追迹系统的表现。因此在优化结果的呈现上，F/3 NIR光学系统会有不错的影像质量，但NIR人眼追迹系统则不然。我们可以在下方的MTF图中看到以完整FOV取样的结果，以及NIR人眼追迹系统中所有视场的像散。后者的平均像散约为1.4个波，并在整个FOV具有1.42个波的RMS平均波前误差。

为了得到各系统较平衡的结果，我们可以重新对三个自由曲面进行优化。但要注意的是，任何增进NIR人眼追迹系统影像质量的改变，都将对显示器系统的成像造成负面的影响。此时，改以TrueFreeForm面进行设计便成了一个更好的选项。如果用户想在不牺牲显示器成像质量的情况下改善人眼追迹系统，可以由S3 （即棱镜最上方的面）的子孔径优化着手。

定义网格矢高变数

注意，在下图中我们可以看到NIR光束在S3上产生成像路径的光迹（footprint， 绿色区域）和微显示器上的光线（蓝色区域）是明显分离的。

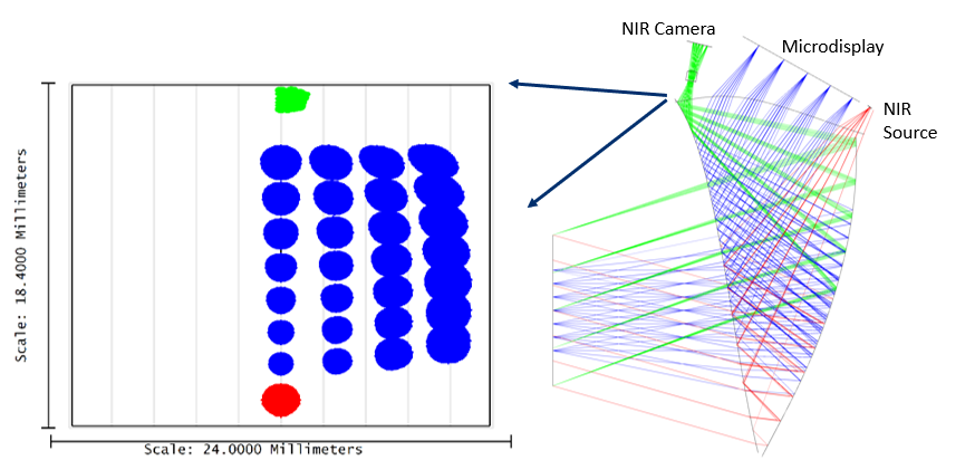
当TrueFreeForm面S3的扩展多项式已根据微显示器系统完成优化，我们接着将网格矢高的信息填入表面矢高的设定中（默认值皆为0）。此时，只剩下S3上接收NIR光束（人眼追迹系统）的区域需被重新优化。需要注意的是，在优化的过程中由微显示器发出、落在S3上的光束所产生的光迹不会受到影响。此外在原先的设计中，与视场无关的像散为主要的像差。因此我们可以使用较低阶的表面轮廓修正明显的改善成像质量。有了以上的认知，我们就可以开始着手进行设计了！

我们首先产生一个空白的网格矢高档案，文件中所有的数值均为0。我们可以善用系统左右对称的特性，仅先针对右半边的网格矢高信息进行优化。接着利用对称功能，使左半边的数值随右半边变化。透过上述的步骤我们可以有效减少变量个数，将变量集中在右半边。

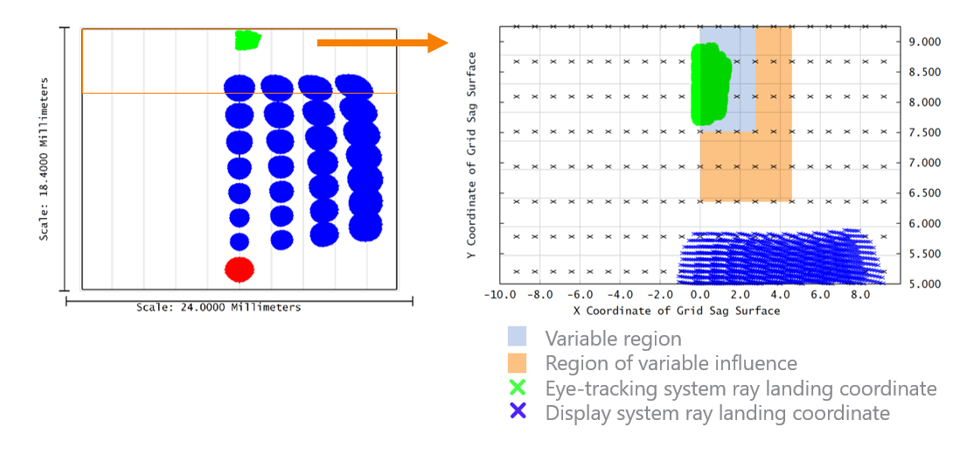
上图中为网格矢高的信息。右图中，所有的数据点均以黑色的“x”表示。我们可以看到浅蓝色、且大小为4x4的范围代表了变数区。在前面的篇幅中曾提到，双三次样条的内差算法将变量影响的范围向外扩增两点，也就是图中的橘色区域。确认了网格的密度和变量区域后，我们可以肯定光学表面的信息会被限制在微显示器的成像范围内，意即微显示系统的表现将在优化的过程被保留。

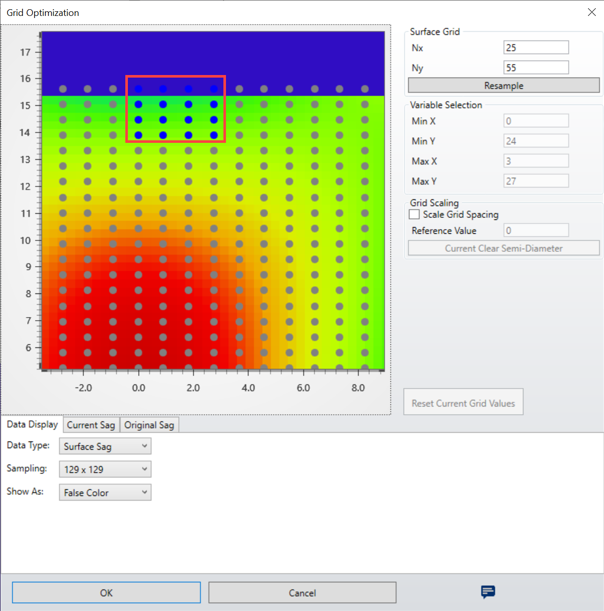
在下图中，我们选取了目标范围内的网格矢高点，且令为变数。

优化网格矢高

在完成网格矢高的定义和变量设定后，我们就可以开始建立优化函数了。我们首先将表面的优化限缩在一个子孔径内，也就是说我们会移除大部分的变量，仅保留网格矢高的数据点和NIR的接收位置。此时所有之前用来优化显示器系统的目标均须被移除。

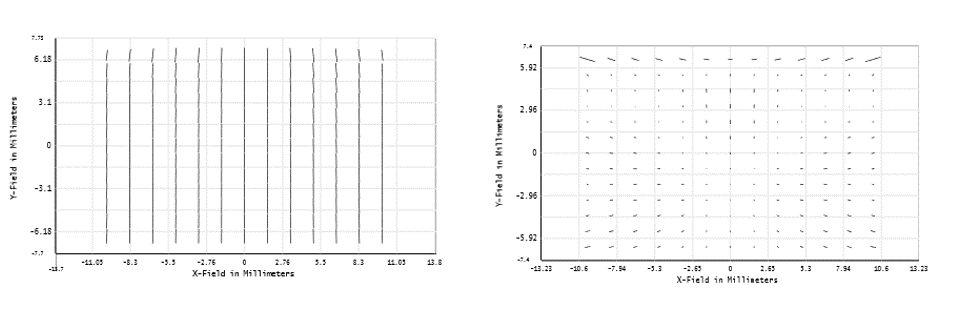
我们以一个预设的优化函数进行优化。在这里要注意的是，在光瞳积分（pupil intgration）设定方面，我们选择以矩形阵列（Rectangular Array）进行设计，而非高斯求积（Gaussian Quadrature），因为后者会使光瞳中大部分的区域不被采样。上述的状况并不是我们乐见的，每个网格变量的影响范围不同可能导致部分视场或光瞳无法被等量的优化。基于以上描述，我们在进行设计时将需要较高的光瞳及视场采样率，避免只有目标中的部分区域被优化（特别是进行焦平面周围区域的优化时，此时的表面上的光迹会因为视场的不同而有明显的间隔）。

在完成视场及光瞳的采样设定后，我们还需要再加入一些关于最大倾斜度（allowed maximum slope）和矢高的限制，而操作数GOPT可以帮助我们顺利达成目的。GOPT检视了网格中的矢高和局部区域的斜率，确保这些数值的最大和最小值都能被限制在合理的范围内。

优化结果

优化结束后，我们可以看到一个局域的矢状面（sagittal）曲率被加入目标的区域中以抵消大部分的像散，同时又使non-local的表面信息维持不变。这样的结果很接近我们原先对矢高的预期。

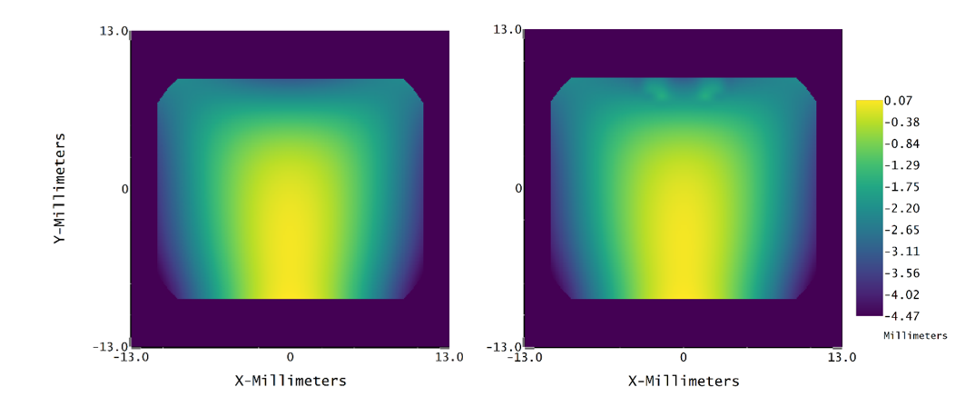
我们可以通过MTF结果观察到微显示器系统在优化前后有相同的表现。这样的结果也证实了网格变量的选择是合理的，且这些变量与NIR人眼追迹系统的优化并不会互相影响。

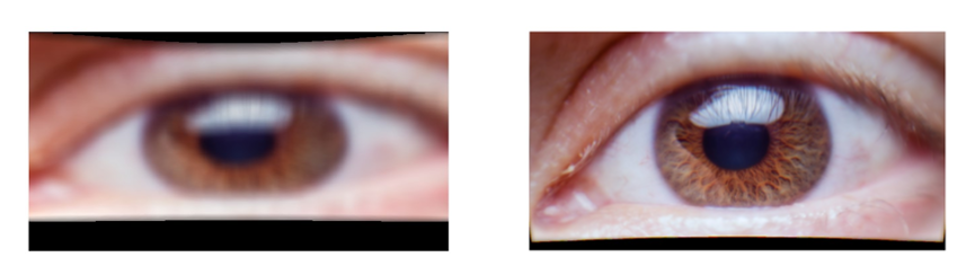
而NIR人眼追迹系统经过优化后，成像的表现有了显著的提升。系统的像散在各视场有了几个数量级的改善（如850 nm处由1.38个波缩小为0.0509个波）。而此系统的MTF表现也有明显的提升（在 40 lp/mm时，平均视场为0.45），用户可以看见清晰的像。这样的结果使我们可以准确的接收用户瞳孔的NIR反射，并据此来帮助在软件中投射影像的优化。

结论

在这篇文章中我们看到了一个网格矢高优化功能可以成功的应用在局部表面的修正及部分光学系统的成像改善，且同时保留了非局部（non-local）的矢高。至于此优化功能的缺点则是用户必须谨慎的设定视场和光瞳的采样以及矢高网格的变量数量。一般而言，这种优化方式会需要较高的光束采样和大量的变量，以至于需要较长的优化时间。

此外，还有一些我们在进行自由曲面优化或制造时需要注意的地方。在建立优化函数时，我们仅使用为数不多的 GOPT 操作数限制变量区内的矢高和斜率。为了使所有的表面维持连续的状况，OpticStudio 会黏合变量区和周围网格矢高结构的边缘，这时就可能出现交界处十分陡峭的情形。范例中的变量区在X方向的长度约为5 mm，我们可以在该表面向外延伸的区域发现斜率急剧变化的现象（准确的来说，延伸区域为向外2个网格点，即变量的影响范围）。如果能确保每个矢高点的影响范围都有合理的斜率，将进一步使我们的设计更理想。我们可以利用 SSAG 操作数或是其他等效的斜率计算方式，达到限制特定区域斜率的目的，例如变量区的 RMS 斜率。